
题目列表(包括答案和解析)
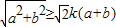 对任意正数a,b恒成立,则实数k的最大值为( )
对任意正数a,b恒成立,则实数k的最大值为( )
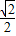
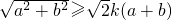 对任意正数a,b恒成立,则实数k的最大值为
对任意正数a,b恒成立,则实数k的最大值为

| a2+b2 |
| 2 |
A、
| ||||
| B、1 | ||||
| C、2 | ||||
D、
|
| a2+b2 |
| 2 |
A.
| B.1 | C.2 | D.
|
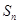 为数列
为数列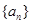 的前
的前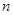 项之和.若不等式
项之和.若不等式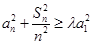 对任何等差数列
对任何等差数列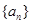 及任何正整数
及任何正整数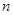 恒成立,则
恒成立,则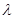 的最大值为
的最大值为 A. | B. | C. | D. |
一、选择:
1―5AADBA 6―10DCBCB 11―12DA
二、填空
13.2 14.(1)(3) 15.
16.4 17.14 18.
三、解答:
19.解:(1)

(2)


20.证明:(1)由三视图可知,平面 平面ABCD,
平面ABCD,
设BC中点为E,连结AE、PE


 ,PB=PC
,PB=PC



|