练习册

  • 练习册
  • 试题
    A． B． C． D． (一)必做题 【查看更多】

     

    题目列表(包括答案和解析)

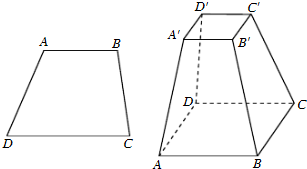    （必做题）先阅读：如图，设梯形ABCD的上、下底边的长分别是a，b（a＜b），高为h，求梯形的面积．
    方法一：延长DA、CB交于点O，过点O作CD的垂线分别交AB、CD于E、F，则EF=h．
    设OE=x，∵△OAB∽△ODC，∴
    x
    x+h
    =
    a
    b
    ，即x=
    ah
    b-a
    ．
    ∴S梯形ABCD=S△ODC-S△OAB=
    1
    2
    b（x+h）-
    1
    2
    ax=
    1
    2
    （b-a）x+
    1
    2
    bh=
    1
    2
    （a+b）h．
    方法二：作AB的平行线MN分别交AD、BC于MN，过点A作BC的平行线AQ分别于MN、DC于PQ，则△AMP∽△ADQ．
    设梯形AMNB的高为x，MN=y，
    x
    h
    =
    y-a
    b-a
    ⇒y=a+
    b-a
    h
    x，∴S梯形ABCD=
    ∫
    h
    0
    （a+
    b-a
    h
    x）dx=（ax+
    b-a
    2h
    x2）
    |
    h
    0
    =ah+
    b-a
    2h
    •h2=
    1
    2
    （a+b）h．
    再解下面的问题：
    已知四棱台ABCD-A′B′C′D′的上、下底面的面积分别是S1，S2（S1＜S2），棱台的高为h，类比以上两种方法，分别求出棱台的体积（棱锥的体积=
    1
    3
    ×底面积×高）．

    查看答案和解析>>

    下列命题中正确的是（    ）

    A．若两条直线都垂直于第三条直线，则这两条直线一定平行；

    B．若两条直线和第三条直线成等角，则这两条直线平行；

    C．与两条异面直线都垂直的直线，叫做异面直线的公垂线；

    D．一直线与两平行线中的一条垂直，则必与另一条也垂直．

     

    查看答案和解析>>

    下列命题中正确的是（    ）

    A．若两条直线都垂直于第三条直线，则这两条直线一定平行；

    B．若两条直线和第三条直线成等角，则这两条直线平行；

    C．与两条异面直线都垂直的直线，叫做异面直线的公垂线；

    D．一直线与两平行线中的一条垂直，则必与另一条也垂直．

     

    查看答案和解析>>

    小明做了两道题，事件A为“做对第一个”，事件B为“做对第二个”，其中“做对第一个”与“做对第二个”的概率都是，下列说法正确的是（　　）

        A．小明做对其中一个的概率为

        B．事件A与事件B为互斥事件

        C．A∩B={两个题都做对}

        D．事件A与事件B必然要发生一个

         

    查看答案和解析>>

    为了解某中学生遵守《中华人民共和国交通安全法》的情况，调查部门在该校进行了如下的随机调查，向被调查者提出两个问题：（1）你的学号是奇数吗？（2）在过路口时你是否闯过红灯？要求被调查者背对着调查人员抛掷一枚硬币，如果出现正面，就回答第一个问题，否则就回答第二个问题．被调查者不必告诉调查人员自己回答的是哪一个问题，只需回答“是”或“不是”，因为只有调查者本人知道回答了哪一个问题，所以都如实地做了回答．结果被调查的800人（学号从1至800）中有240人回答了“是”．由此可以估计这800人中闯过红灯的人数是（　　）

    查看答案和解析>>

     

    一、选择：

    1―5AADBA  6―10DCBCB  11―12DA

    二、填空

    13．2   14．（1）（3）  15．

    16．4  17．14  18．

    三、解答：

    19．解：（1）

          

       （2）

          

          

    20．证明：（1）由三视图可知，平面平面ABCD，

           设BC中点为E，连结AE、PE

          

          

           ，PB=PC

          

          

          

    //

    //

    //

          

    四边形CHFD为平行四边形，CH//DF

          

           又

           平面PBC

          

           ，DF平面PAD

           平面PAB

    21．解：设

          

          

           对成立，

           依题有成立

           由于成立

              ①

           由于成立

             

           恒成立

              ②

           综上由①、②得

     

     

    22．解：设列车从各站出发时邮政车厢内的邮袋数构成数列

       （1）

           在第k站出发时，前面放上的邮袋个

           而从第二站起，每站放下的邮袋个

           故

          

           即从第k站出发时，共有邮袋

       （2）

           当n为偶数时，

           当n为奇数时，

    23．解：①

           上为增函数

           ②增函数

          

          

          

          

          

           同理可证

          

          

    24．解：（1）假设存在满足题意

           则

          

           均成立

          

          

           成立

           满足题意

       （2）

          

          

          

          

           当n=1时，

          

           成立

           假设成立

           成立

           则

          

          

          

          

          

          

          

          

          

          

           即得成立

           综上，由数学归纳法可知

     

     

     


    同步练习册答案