
题目列表(包括答案和解析)
已知定义在R上的函数![]() 满足
满足![]() ,且对任意的
,且对任意的![]()
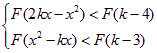 均成立,(1)求证:函数
均成立,(1)求证:函数![]() 在R上为减函数(2)求实数k的取值范围。
在R上为减函数(2)求实数k的取值范围。
已知定义在R上的函数![]() 满足
满足![]() ,且对任意的
,且对任意的![]()
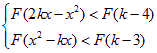 均成立,(1)求证:函数
均成立,(1)求证:函数![]() 在R上为减函数(2)求实数k的取值范围。
在R上为减函数(2)求实数k的取值范围。
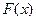 满足
满足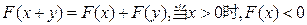 ,且对任意的
,且对任意的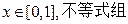
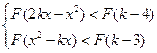 均成立,(1)求证:函数
均成立,(1)求证:函数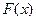 在R上为减函数(2)求实数k的取值范围。
在R上为减函数(2)求实数k的取值范围。已知定义在R上的函数![]() 满足条件
满足条件![]() ,且函数
,且函数![]() 是奇函数,给出以下四个命题:
是奇函数,给出以下四个命题:![]() ①函数
①函数![]() 是周期函数;
是周期函数;![]() ②函数
②函数![]() 的图象关于点
的图象关于点![]() 对称;
对称;![]()
③函数![]() 是偶函数;
是偶函数;![]() ④函数
④函数![]() 在R上是单调函数.
在R上是单调函数.![]() 在上述四个命题中,真命题的序号是___(写出所有真命题的序号)。
在上述四个命题中,真命题的序号是___(写出所有真命题的序号)。![]()
一、选择:
1―5AADBA 6―10DCBCB 11―12DA
二、填空
13.2 14.(1)(3) 15.
16.4 17.14 18.
三、解答:
19.解:(1)

(2)


20.证明:(1)由三视图可知,平面 平面ABCD,
平面ABCD,
设BC中点为E,连结AE、PE


 ,PB=PC
,PB=PC



|