
题目列表(包括答案和解析)
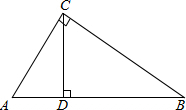 线与△ABC的直角边相交于点F,设AE=x,△AEF的面积为y.
线与△ABC的直角边相交于点F,设AE=x,△AEF的面积为y. 线与△ABC的直角边相交于点F,设AE=x,△AEF的面积为y.
线与△ABC的直角边相交于点F,设AE=x,△AEF的面积为y.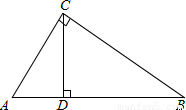
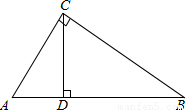

一、选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
A
D
C
A
C
B
C
D
D
A
二、填空题
题号
11
12
13
14
15
16
答案
+1与-1(答案不唯一)
b (b-2)
3n
.files/image143.gif)
③
三、解答题:
17、原式=6 18、.files/image145.gif) 19、
19、.files/image147.gif)
20、(略)
21、∵BC=CD ∴∠CBD=∠CDB ∵AD∥BC ∴ ∠CBD=∠ADB ∴∠CDB=∠ADB
又∵BE⊥DC ∴∠BDE=.files/image149.gif) 又∵∠A=
又∵∠A=.files/image149.gif) ∴∠BED=∠A 又∵BD=BD
∴∠BED=∠A 又∵BD=BD
∴△ABD≌△EBD
四、解答题:
22、(1)黄球概率.files/image151.gif) . (2)(略)
. (2)(略)
23、(1)k=8 (2)点(―2,―4)在双曲线上
24、约等于
25、(1)①②③结论正确(2)(略)
五、解答题
26、(1)频率0.5;频数50 (2)(3)略
27、(1).files/image153.gif) (2)线段GB与DF的大小相等、位置关系垂直
(2)线段GB与DF的大小相等、位置关系垂直
证明△DCF≌△GCB,实际△DCF绕着点O旋转.files/image149.gif) 所得△GCB
所得△GCB
28、解:(1).files/image156.gif) 抛物线
抛物线.files/image158.gif) 过
过.files/image160.gif) ,
,
.files/image162.gif)
.files/image156.gif) 点
点.files/image130.gif) 在抛物线上,
在抛物线上,
.files/image166.gif) ,
,
.files/image168.gif) 点
点.files/image130.gif) 的坐标为
的坐标为.files/image171.gif) .
.
(2)由(1)得.files/image173.gif) (
(.files/image175.gif) ),
),.files/image177.gif) ,在Rt△AEF中,
,在Rt△AEF中,.files/image179.gif) ,
,.files/image181.gif)
∴.files/image183.gif) 解得
解得.files/image185.gif) .
.
(3).files/image141.gif) 的面积有最大值,
的面积有最大值,
.files/image188.gif) 的对称轴为
的对称轴为.files/image190.gif) ,
,.files/image160.gif) ,
,.files/image168.gif) 点
点.files/image194.gif) 的坐标为
的坐标为.files/image196.gif) ,
,
由(1)得.files/image198.gif) ,
,
而.files/image200.gif)
.files/image202.gif)
=.files/image204.gif)
.files/image206.gif) ,
, .files/image208.gif) 的对称轴是
的对称轴是.files/image210.gif) ,
,.files/image212.gif)
.files/image168.gif) 当
当.files/image215.gif) 时,
时,.files/image217.gif) 取最大值,
取最大值,
其最大值为.files/image219.gif) .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com