练习册

  • 练习册
  • 试题
    36(Ⅲ) 的数学希望为. 【查看更多】

     

    题目列表(包括答案和解析)

    18、某运动员射击一次所得环数X的分布如下：

    现进行两次射击，以该运动员两次射击中最高环数作为他的成绩，记为ξ
    （Ⅰ）求该运动员两次都掵中7环的概率；
    （Ⅱ）求ξ的分布列．
    （Ⅲ）求ξ的数学希望

    查看答案和解析>>

    某运动员射击一次所得环数X的分布列如下：

    X

    0～6

    7

    8

    9

    10

    Y

    0

    0.2

    0.3

    0.3

    0.2

    现进行两次射击，以该运动员两次射击中最高环数作为他的成绩，记为ξ.

    (1)求该运动员两次都命中7环的概率；

    (2)求ξ分布列；

    (3)求ξ的数学希望.

     

     

    查看答案和解析>>

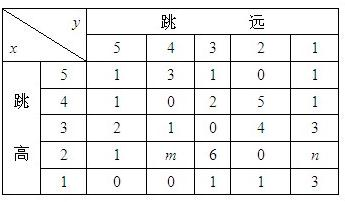    精英家教网下表为某体育训练队跳高与跳远成绩的统计表，全队有队员40人，成绩分为1分至5分五个档次，例如表中所示：跳高成绩为4分的人数是：1+0+2+5+1=9人；跳远成绩为2分的人数是：0+5+4+0+1=10人；跳高成绩为4分且跳远成绩为2分的队员为5人．
    将记载着跳高、跳远成绩的全部队员的姓名卡40张混合在一起，任取一张，记该卡片队员的跳高成绩为x，跳远成绩为y，设x，y为随机变量（注：没有相同姓名的队员）
    （1）求m+n的值；
    （2）求x=4的概率及x≥3且y=5的概率；
    （3）若y的数学期望为
    10540
    ，求m，n的值．

    查看答案和解析>>

    有A，B，C，D四个城市，它们各有一个著名的旅游点依此记为a，b，c，d．把A，B，C，D和a，b，c，d分别写成左、右两列，现在一名旅游爱好者随机用4条线把左右全部连接起来，构成“一一对应”，如果某个旅游点是与该旅游点所在的城市相连的（比如A与a相连）就得2分，否则就得0分；则该爱好者得分的数学期望为
    2分
    2分
    ．

    查看答案和解析>>

    11、某投篮游戏规定：每轮至多投三次，直到首次命中为止．第一次就投中，得8分；第一次不中且第二次投中，得6分；前两次均不中且第三次投中，得4分；三次均不中，得0分．若某同学每次投中的概率为0.5，则他每轮游戏的得分X的数学期望为
    6
    ．

    查看答案和解析>>


    同步练习册答案