题目列表(包括答案和解析)
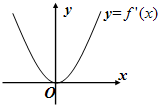已知f（x）是定义域为R的奇函数，f（-4）=-1，f（x）的导函数f′（x）的图象如图所示．若两正数a，b满足f（a+2b）＜1，则| a+2 |
| b+2 |
A、(
| ||
B、(
| ||
| C、（-1，10） | ||
| D、（-∞，-1） |
已知f（x）是定义域为R的奇函数，f（-4）=-2，f（x）的导函数f′（x）的图象如图所示，若两正数a，b满足f（a+2b）＜2，则| a+4 |
| b+4 |
| 2x-1 | 2x+1 |
一、选择题：
1.A 2.B 3.C 4.C 5.D 6.A 7.D 8.C 9.D 10.D 11.A 12.B
二、填空题：
13．14 14．2 15．30 16．①③
17. -1 18. －5 19． -1-
20. 
21． 4 22．
23．10 24．412 25．①④
三、解答题：
26解：（1）
，
由
，有
，
解得
。
（2）解法一：
。
解法二：由（1），，得
∴
∴
于是
，
代入得
。
27证明：（1）∵
∴
（2）令
中点为
，
中点为
，连结
、
∵是
的中位线
∴
又∵
∴
∴
∴
∵
为正
∴
∴
又∵
，
∴四边形
为平行四边形
∴
∴
28解：（1）设
米，
，则
∵
∴
∴
∴
∴
∴
∴
或
（2）
此时
（3）∵
令
，
∵
当
时，
∴在
上递增
∴
此时
答：（1）
或
（2）当
的长度是
的面积最小，最小面积为
（3）当的长度是的面积最小，最小面积为
29解：（1）①若直线
的斜率不存在，即直线是
，符合题意。
②若直线斜率存在，设直线为
，即
。
由题意知，圆心
以已知直线的距离等于半径2，即：
，
解之得
所求直线方程是，
（2）解法一：直线与圆相交，斜率必定存在，且不为0，可设直线方程为
由
得
又直线
与垂直，由
得
∴
为定值。
故
是定值，且为6。
30解：（1）由题意得
，
∴
，
∴
∴
，∴
在
是
单调增函数，
∴
对于
恒成立。
（3） 
方程
；
（4） ∴
∵
，∴方程为
令
，
，
∵
，当
时，
，
∴
在
上为增函数；
时，
，
∴在
上为减函数，
当
时，
，
∴函数
、
在同一坐标系的大致图象如图所示，
∴①当
，即
时，方程无解。
②当
，即
时，方程有一个根。
③当
，即
时，方程有两个根
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com