
题目列表(包括答案和解析)
本题满分14分)已知函数![]() ,
,![]() ,其中
,其中![]() .w.w.w.k.s.5.u.c.o.m
.w.w.w.k.s.5.u.c.o.m ![]()
![]()
(I)设函数![]() .若
.若![]() 在区间
在区间![]() 上不单调,求
上不单调,求![]() 的取值范围;
的取值范围;
(II)设函数![]() 是否存在
是否存在![]() ,对任意给定的非零实数
,对任意给定的非零实数![]() ,存在惟一的非零实数
,存在惟一的非零实数![]() (
(![]() ),使得
),使得![]() 成立?若存在,求
成立?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本题满分14分) 若F1、F2为双曲线![]() 的左、右焦点,O为坐标原点,P在双曲线左支上,M在右准线上,且满足
的左、右焦点,O为坐标原点,P在双曲线左支上,M在右准线上,且满足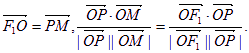 (Ⅰ)求此双曲线的离心率;(Ⅱ)若此双曲线过点
(Ⅰ)求此双曲线的离心率;(Ⅱ)若此双曲线过点![]() ,求双曲线方程;(Ⅲ)设(Ⅱ)中双曲线的虚轴端点为B1,B2(B1在y轴正半轴上),求B2作直线AB与双曲线交于A、B两点,求
,求双曲线方程;(Ⅲ)设(Ⅱ)中双曲线的虚轴端点为B1,B2(B1在y轴正半轴上),求B2作直线AB与双曲线交于A、B两点,求![]() 时,直线AB的方程.
时,直线AB的方程.
(本题满分14分)某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层,每层2000平方米的楼房。经测算,如果将楼房建为x(x ≥ 10)层,则每平方米的平均建筑费用为560 + 48x(单位:元).⑴写出楼房平均综合费用y关于建造层数x的函数关系式;
⑵该楼房应建造多少层时,可使楼房每平方米的平均综合费用最少?最少值是多少?
(注:平均综合费用 = 平均建筑费用 + 平均购地费用,平均购地费用 = )
 (本题满分14分)如图,已知二次函数
(本题满分14分)如图,已知二次函数![]() ,直线l
,直线l![]() :x = 2,直线l
:x = 2,直线l![]() :y = 3tx(其中
:y = 3tx(其中![]() 1< t < 1,t为常数);若直线l
1< t < 1,t为常数);若直线l![]() 、l
、l![]() 与函数
与函数![]() 的图象所围成的封闭图形如图(5)阴影所示.(1)求y =
的图象所围成的封闭图形如图(5)阴影所示.(1)求y = ![]() ;(2)求阴影面积s关于t的函数s = u(t)的解析式;(3)若过点A(1,m)(m≠4)可作曲线s=u(t)(t∈R)的三条切线,求实数m的取值范围.
;(2)求阴影面积s关于t的函数s = u(t)的解析式;(3)若过点A(1,m)(m≠4)可作曲线s=u(t)(t∈R)的三条切线,求实数m的取值范围.
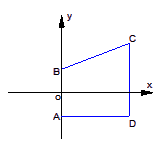 (本题满分14分)
(本题满分14分)
在梯形ABCD中,AB⊥AD,AB∥CD,A、B是两个定点,其坐
标分别为(0,-1)、(0,1),C、D是两个动点,且满足|CD|=|BC|.
(1)求动点C的轨迹E的方程;
(2)试探究在轨迹E上是否存在一点P?使得P到直线y=x-2的
距离最短;
(3)设轨迹E与直线![]() 所围成的图形的
所围成的图形的
面积为S,试求S的最大值。
其它解法请参照给分。
说明:
1.本解答给出的解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.
2.对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.
3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.
4.只给整数分数,填空题不给中间分数.
一、填空题(本大题共14小题,每小题5分,共70分)
1.{0,1} 2.1 3.2 4.-3 5.5 6.[2,5]
7.60 8.4 9. 10.(,) 11. 12.4
13. 14.(,]
二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤)
15.(本题满分14分)
解:(1)tana==,…………………………………………3分
所以=,又因为sin2a+cos2a=1,
解得sina=.………………………………………………………7分
(2)因为0<a<<b<p,所以0<b-a<p.
因为cos(b-a)=,所以sin(b-a)=.……………………9分
所以sinb=sin[(b-a)+a]
=sin(b-a)cosa+cos(b-a)sina=×+×=,……12分
因为b∈(,p),
所以b=.………………………………………………………14分
16.(本题满分14分)
证明:(1)取AB1中点F,连结DF,CF.因为D为A1B1中点,
所以DF∥=AA1.
因为E为CC1中点,AA1∥=CC1,
所以CE∥=DF.
所以四边形CFDE为平行四边形.
所以DE∥CF.…………………………………………………4分
因为CFÌ平面ABC,DE(/平面ABC,
所以DE∥平面ABC.…………………………………………7分
(2) 因为AA
因为BB
因为AC∶AB∶CC1=3∶5∶4,
所以AC∶AB∶BC=3∶5∶4,
所以AC2+BC2=AB2.……………………………………10分
所以AC^BC.
所以AC^平面BB
所以AC^BC1.
所以BC1^平面AB
 |
17.(本题满分14分)
解:(1)设从A地运出的油量为a,根据题设,直接运油到B地,往返油耗等于a,
所以B地收到的油量为(1-)a.
所以运油率P1==.……………………………………3分
而从A地运出的油量为a时,C地收到的油量为(1-)a,
B地收到的油量(1-)(1-)a,
所以运油率P2=
=(1-)(1-)=(+)(1-).…………………………7分
所以P2-P1=x(1-x),因为0<x<1,
所以P2-P1>0,即P2>P1.…………………………………………9分
(2)因为P2=(+)(1-)≤=.
当且仅当+=1-,即x=时,取“=”.
所以当C地为AB中点时,运油率P2有最大值.……………………………………14分
18.(本题满分16分)
解:(1)因为抛物线顶点在原点,准线方程为x=-1,
所以抛物线开口向右,且-=-1,所以p=2.
所以所求的抛物线方程为y2=4x.…………………………………………4分
(2)设P(x0,y0),则y02=4x0,半径r=PF=x0+1,
圆P的方程为(x-x0)2+(y-y0)2=(x0+1)2,……………………………6分
设AB的方程为y=2x+b,由AB=2CD得,
圆心P到直线AB的距离2d=,……………………………6分
所以5d2=r2,即d=r.
因为r=|x0+1|,d=,
代入得ㄏ2x0-y0+bㄏ=ㄏx0+1ㄏ.…………………………………8分
即2x0-y0+b=x0+1或2x0-y0+b=-x0-1.
所以x0-y0+b-1=0或3x0-y0+b+1=0.
因为y02=4x0,所以x0=y02,
代入得y02-y0+(b-1)=0或y02-y0+(b+1)=0.……………………10分
方程y02-y0+(b-1)=0关于y0有解Û1-(b-1)≥0,b≤2.
方程y02-y0+(b+1)=0.关于y0有解Û1-3(b+1)≥0,b≤-.…12分
综上所述,b的最大值为2.……………………………………………14分
此时,y0=2,x0=1,r=x0+1=2,
所以圆P的方程为(x-1)2+(y-2)2=4.……………………………16分
19.(本题满分16分)
解: f ¢(x)=(x>0) 2分
(1)由已知,得f ¢(x)在[1,+∞)上有解,即a=在(1,+∞)上有解,
又 当x∈(1,+∞)时,<1,
当x∈(1,+∞)时,<1,
所以a<1.又a>0,所以a的取值范围是(0,1).………………………………6分
(2)①当a≥时,
因为f ¢(x)>0在(e,e2)上恒成立,这时f(x)在[e,e2]上为增函数,
所以当x=e时,f(x)min=f(e)=1+ ……………………………………………… 8分
②当0<a≤时,
因为f ¢(x)<0在(e,e2)上恒成立,
这时f(x)在[e,e2]上为减函数,
所以,当x=e2时,f(x)min=f(e2)=2-,…………………………………………10分
③当<a<时,令f¢(x)=0得,x=∈(e,e2),
又因为对于x∈(e,)有f ¢(x)<0,
对于x∈(,e2)有f ¢(x)>0,
所以当x=时,f(x)min=f()=ln+1-.………………………………………14分
综上,f(x)在[e,e2]上的最小值为
f(x)min=………………………………………16分
20.(本题满分16分)
解:(1)由条件得an+2=(2+)an+1-an,
所以an+2-an+1=2(an+1-an),
即bn+1=2bn,又b1=a2-a1=2,所以bn≠0,
从而=2对n∈N*成立,
所以数列{bn}是首项为b1=2,公比q=2的等比数列,
所以bn=2n.…………………………………………………6分
(2)由(1)得an+1―an=2n.所以(n+1)an+1-nan=(n+1)×2n,………………8分
所以
…………,
nan-(n-1)an-1=n×2n-1,
相加得nan-a1=2×21+3×22+4×23+…+n×2n-1,
所以2(nan-a1)= 2×22+3×23+…+(n-1)×2n-1+n×2n.
两式相减得:-(nan-a1)=2(21+22+…+2n-1)-n×2n=2n+1-4-n×2n,所以
an=2n-=.…………………………………………………………11分
(3)因为cn===4[-],…………13分
所以Sn=c1+c2+…+cn
=4[-+-+-+…+-]
=4[-]=2-<2.…………………………………………………16分
南京市第十三中学2009届高三年级第三次模拟考试
数学附加卷答案 2009.5
1.(几何证明选讲)(本题满分10分)
证明:证明:因为A,B,C,D四点共圆,所以ÐADF=ÐABC.
因为PF∥BC,所以ÐAFP=ÐABC.所以ÐAFP=ÐFQP.
因为ÐAPF=ÐFPA,所以△APF∽△FPQ.所以=.………………5分
所以PF2=PA×PD.因为PQ与圆相切,所以PQ2=PA×PD.
所以PF2=PQ2.所以PF=PQ.……………………………………………10分
2.(矩阵与变换)(本题满分10分)
解:∵MN= =,
设直线y=2x+1上一点(x0,y0)在MN作用下变为(x¢,y¢),则
=, 即=,即
从而可得……………………………………5分
∵y0=2x0+1,代入得y¢=2(x¢-y¢)+1,
化简得2x¢-y¢+1=0,即6x¢-5y¢+3=0.
即变换后的直线方程是6x-5y+3=0.…………………………10分
3.(坐标系与参数方程)(本题满分10分)
解:⊙O的直角坐标方程是x2+y2-x-y=0,
即(x-)2+(y-)2=.………………………………………………3分
直线l的极坐标方程为r(cosq-sinq)=4,
直线l的直角坐标方程为x-y-4=0.………………………………6分
设M(+cosq,+sinq)为⊙C上任意一点,M点到直线l的距离
d==,
当q=时,dmin=.…………………………………………………10分
4.(不等式选讲)(本题满分10分)
解:因为++≥3=3,………………………………………4分
所以ㄏx+1ㄏ+ㄏx-1ㄏ≤3,
x∈[-,].…………………………………………………………10分
5.(本题满分10分)
解:解:(1)选取的5只恰好组成完整“奥运会吉祥物”的概率
 ………………………………………………3分
………………………………………………3分
(2)ξ的取值为100,80,60,40.…………………………………4分

 ……………………………………………………8分
……………………………………………………8分
ξ的分布列为
ξ
100
80
60
40




……………………………………………………………………………………9分
Eξ= …………………………………………10分
…………………………………………10分
6.(本题满分10分)
解:(1)∵ ,∴
,∴ .
.
∴ (
( ).
).
∴ (
( ).
).
∴ (
( ).
).
∴ (
( ).
).
∴ 数列
数列 为等比数列,其公比为
为等比数列,其公比为 ,首项
,首项 ,
,
而 ,且
,且 ,∴
,∴ .
.
∴ .
.
∴ .…………………………………………………………4分.
.…………………………………………………………4分.
(2)∵
 ,
,
∴  .
.
∴
 .
.
∴
 , ①
, ①
∴ 2
2
 . ②
. ②
①-②得 -
 ,
,

 ,
,
∴
 .…………………………………………………6分.
.…………………………………………………6分.
∴ (
( )=
)= =
= .
.
当 时,
时, =
= ;
;
当 时,
时, -(
-( )=4(4-5)=-4
)=4(4-5)=-4 ,
,

 ;
;
当 时,
时, ,
,
且
 ,
,
∴ 时,总有
时,总有 .…………………………………………………10分.
.…………………………………………………10分.
∴ 时,总有
时,总有

 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com