
题目列表(包括答案和解析)
 如图,椭圆中心在坐标原点,F为左焦点,当
如图,椭圆中心在坐标原点,F为左焦点,当| FB |
| AB |
| ||
| 2 |
 如图,椭圆中心在坐标原点,焦点在坐标轴上,A、B是顶点,F是左焦点;当BF⊥AB时,此类椭圆称为“黄金椭圆”,其离心率为
如图,椭圆中心在坐标原点,焦点在坐标轴上,A、B是顶点,F是左焦点;当BF⊥AB时,此类椭圆称为“黄金椭圆”,其离心率为
| ||
| 2 |
 如图,椭圆中心在坐标原点,F为左焦点,当
如图,椭圆中心在坐标原点,F为左焦点,当| FB |
| AB |
| ||
| 2 |
如图,椭圆中心在坐标原点,F为左焦点,A为右顶点,B为上顶点,当![]() 时,其离心率为
时,其离心率为![]() ,此类椭圆被称为“黄金椭圆”。类比黄金椭圆,可推算出“黄金双曲线”的离心率e等于 。
,此类椭圆被称为“黄金椭圆”。类比黄金椭圆,可推算出“黄金双曲线”的离心率e等于 。

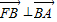 时,椭圆被称为“黄金椭圆”,则“黄金椭圆”的离心率e等于( )
时,椭圆被称为“黄金椭圆”,则“黄金椭圆”的离心率e等于( )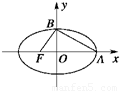
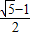
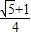
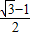
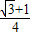
一、选择题
DDDCC CDAAB
二、填空题
11、.files\image321.gif) 12、
12、.files\image323.gif) 13、
13、.files\image325.gif) 14、17 0 15、②③
14、17 0 15、②③
三、解答题
16、⑴.files\image327.gif)
.files\image329.gif)
.files\image331.gif)
.files\image333.gif)
17、(1).files\image335.gif) ,其定义域为
,其定义域为.files\image337.gif) .
.
.files\image339.gif) 令
令.files\image341.gif) 得
得.files\image343.gif) .……………………………………………………2′
.……………………………………………………2′
当.files\image345.gif) 时,
时,.files\image347.gif) 当
当.files\image349.gif) 时,
时,.files\image351.gif) 故当且仅当
故当且仅当.files\image353.gif) 时,
时,.files\image355.gif) . 6′
. 6′
(2).files\image357.gif)
由(1)知.files\image359.gif) ≤
≤.files\image048.gif) ,
,
.files\image362.gif) ≥
≥.files\image364.gif) …………………………9′
…………………………9′
又.files\image366.gif)
.files\image368.gif) 故
故.files\image370.gif) …………………………………………12′′18、(1)符合二项分布
…………………………………………12′′18、(1)符合二项分布.files\image372.gif)
.files\image374.gif)
0
1
2
3
4
5
6
……6′
.files\image177.gif)
.files\image377.gif)
.files\image379.gif)
.files\image377.gif)
.files\image382.gif)
.files\image377.gif)
.files\image384.gif)
.files\image377.gif)
.files\image386.gif)
.files\image377.gif)
.files\image388.gif)
.files\image377.gif)
.files\image377.gif)
(2).files\image374.gif) 可取15,16,18.
可取15,16,18.
.files\image390.gif) 表示胜5场负1场,
表示胜5场负1场,.files\image392.gif) ;………………………………7′
;………………………………7′
.files\image394.gif) 表示胜5场平1场,
表示胜5场平1场,.files\image396.gif) ;………………………………8′
;………………………………8′
.files\image398.gif) 表示6场全胜,
表示6场全胜,.files\image400.gif) .……………………………………………9′
.……………………………………………9′
∴.files\image402.gif) .………………………………………………………………12(
.………………………………………………………………12(
19、解:(1)以.files\image404.gif) 所在直线为
所在直线为.files\image048.gif) 轴,以
轴,以.files\image407.gif) 所在直线为
所在直线为.files\image050.gif) 轴,以
轴,以.files\image410.gif) 所在直线为
所在直线为.files\image188.gif) 轴,建立如图所示的空间直角坐标系,由题意可知
轴,建立如图所示的空间直角坐标系,由题意可知.files\image413.gif) 、
、.files\image415.gif) 、
、.files\image417.gif) ………2′
………2′
.files\image419.gif) 令
令.files\image421.gif)
.files\image423.gif)
.files\image425.gif) 的坐标为
的坐标为.files\image427.gif)
.files\image429.gif)
.files\image431.gif) ,
, .files\image433.gif)
.files\image435.gif)
.files\image437.gif)
.files\image439.gif)
.files\image441.gif)
.files\image443.gif) 而
而.files\image445.gif) ,
,.files\image447.gif)
.files\image449.gif) 是
是.files\image451.gif) 与
与.files\image247.gif) 的公垂线…………………………………………………………4′
的公垂线…………………………………………………………4′
(2)令面.files\image454.gif) 的法向量
的法向量.files\image456.gif) 而
而.files\image458.gif) ,
,.files\image460.gif)
.files\image462.gif) 令
令.files\image464.gif) ,则
,则.files\image466.gif) ,即
,即.files\image468.gif) 而面
而面.files\image470.gif) 的法向量
的法向量.files\image472.gif)
.files\image474.gif) ……6′ ∴二面角
……6′ ∴二面角.files\image476.gif) 的大小为
的大小为.files\image478.gif) .……8′
.……8′
(3).files\image480.gif) 面
面.files\image482.gif) 的法向量为
的法向量为.files\image484.gif)
.files\image486.gif) 到面
到面.files\image488.gif) 的距离为
的距离为
.files\image490.gif) 即
即.files\image251.gif) 到面
到面.files\image488.gif) 的距离为
的距离为.files\image493.gif) .…………12′
.…………12′
20、解:(1)假设存在.files\image261.gif) ,使
,使.files\image263.gif) ,则
,则.files\image495.gif) ,同理可得
,同理可得.files\image497.gif) ,以此类推有
,以此类推有.files\image499.gif) ,这与
,这与.files\image259.gif) 矛盾。则不存在
矛盾。则不存在.files\image261.gif) ,使
,使.files\image263.gif) .……3分
.……3分
(2)∵当.files\image269.gif) 时,
时,.files\image501.gif)
又.files\image503.gif) ,
,.files\image259.gif) ,则
,则.files\image505.gif)
∴.files\image507.gif) 与
与.files\image509.gif) 相反,而
相反,而.files\image511.gif) ,则
,则.files\image513.gif) .以此类推有:
.以此类推有:
.files\image515.gif) ,
,.files\image517.gif) ;……7分
;……7分
(3)∵当.files\image269.gif) 时,
时,.files\image503.gif) ,
,.files\image259.gif) ,则
,则.files\image519.gif)
∴.files\image521.gif) …9分
…9分
∴.files\image523.gif) (
(.files\image269.gif) )……10分
)……10分
∴.files\image526.gif) .……12分
.……12分
.files\image527.gif)
21、解(1)设.files\image529.gif) 则
则.files\image531.gif)
①.files\image533.gif) ②
②.files\image535.gif)
①-②得.files\image537.gif)
.files\image539.gif) ……………………2′
……………………2′
.files\image541.gif) 直线
直线.files\image279.gif) 的方程是
的方程是.files\image544.gif) 整理得
整理得.files\image546.gif) ………………4′
………………4′
(2)联立.files\image548.gif) 解得
解得.files\image550.gif)
设.files\image552.gif)
则.files\image554.gif) 且
且.files\image556.gif) 的方程为
的方程为.files\image558.gif) 与
与.files\image560.gif) 联立消去
联立消去.files\image050.gif) ,整理得
,整理得
.files\image563.gif) ………………………………6′
………………………………6′
.files\image565.gif)
.files\image567.gif)
.files\image569.gif)
.files\image571.gif)
.files\image573.gif) 又
又.files\image575.gif)
.files\image577.gif) …………………………………………8′
…………………………………………8′
(3)直线.files\image305.gif) 的方程为
的方程为.files\image580.gif) ,代入
,代入.files\image560.gif) ,得
,得.files\image583.gif) 即
即
.files\image585.gif) ………………………………………………10′
………………………………………………10′
.files\image587.gif) 三点共线,
三点共线,.files\image589.gif) 三点共线,且
三点共线,且.files\image177.gif) 在抛物线的内部。
在抛物线的内部。
令.files\image307.gif) 为
为.files\image593.gif) 、
、.files\image309.gif) 为
为.files\image596.gif)
故由.files\image317.gif) 可推得
可推得.files\image599.gif)
而.files\image601.gif)
.files\image603.gif)
.files\image605.gif) 同理可得:
同理可得:.files\image607.gif)
.files\image609.gif)
而.files\image599.gif) 得
得.files\image612.gif) ………………………………14′
………………………………14′
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com