
题目列表(包括答案和解析)
已知抛物线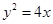 和点
和点 ,过点P的直线
,过点P的直线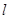 与抛物线交与
与抛物线交与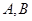 两点,设点P刚好为弦
两点,设点P刚好为弦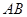 的中点。
的中点。
(1)求直线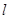 的方程
的方程
(2)若过线段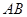 上任一
上任一 (不含端点
(不含端点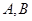 )作倾斜角为
)作倾斜角为 的直线
的直线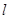 交抛物线于
交抛物线于 ,类比圆中的相交弦定理,给出你的猜想,若成立,给出证明;若不成立,请说明理由。
,类比圆中的相交弦定理,给出你的猜想,若成立,给出证明;若不成立,请说明理由。
(3)过P作斜率分别为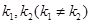 的直线
的直线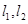 ,
,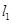 交抛物线于
交抛物线于 ,
,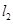 交抛物线于
交抛物线于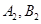 ,是否存在
,是否存在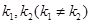 使得(2)中的猜想成立,若存在,给出
使得(2)中的猜想成立,若存在,给出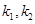 满足的条件。若不存在,请说明理由。
满足的条件。若不存在,请说明理由。
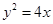 和点
和点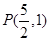 ,过点P的直线
,过点P的直线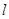 与抛物线交与
与抛物线交与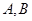 两点,设点P刚好为弦
两点,设点P刚好为弦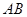 的中点。
的中点。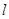 的方程
的方程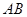 上任一
上任一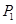 (不含端点
(不含端点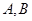 )作倾斜角为
)作倾斜角为 的直线
的直线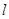 交抛物线于
交抛物线于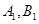 ,类比圆中的相交弦定理,给出你的猜想,若成立,给出证明;若不成立,请说明理由。
,类比圆中的相交弦定理,给出你的猜想,若成立,给出证明;若不成立,请说明理由。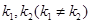 的直线
的直线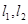 ,
,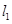 交抛物线于
交抛物线于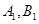 ,
,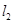 交抛物线于
交抛物线于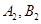 ,是否存在
,是否存在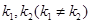 使得(2)中的猜想成立,若存在,给出
使得(2)中的猜想成立,若存在,给出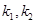 满足的条件。若不存在,请说明理由。
满足的条件。若不存在,请说明理由。一、选择题
DDDCC CDAAB
二、填空题
11、.files\image321.gif) 12、
12、.files\image323.gif) 13、
13、.files\image325.gif) 14、17 0 15、②③
14、17 0 15、②③
三、解答题
16、⑴.files\image327.gif)
.files\image329.gif)
.files\image331.gif)
.files\image333.gif)
17、(1).files\image335.gif) ,其定义域为
,其定义域为.files\image337.gif) .
.
.files\image339.gif) 令
令.files\image341.gif) 得
得.files\image343.gif) .……………………………………………………2′
.……………………………………………………2′
当.files\image345.gif) 时,
时,.files\image347.gif) 当
当.files\image349.gif) 时,
时,.files\image351.gif) 故当且仅当
故当且仅当.files\image353.gif) 时,
时,.files\image355.gif) . 6′
. 6′
(2).files\image357.gif)
由(1)知.files\image359.gif) ≤
≤.files\image048.gif) ,
,
.files\image362.gif) ≥
≥.files\image364.gif) …………………………9′
…………………………9′
又.files\image366.gif)
.files\image368.gif) 故
故.files\image370.gif) …………………………………………12′′18、(1)符合二项分布
…………………………………………12′′18、(1)符合二项分布.files\image372.gif)
.files\image374.gif)
0
1
2
3
4
5
6
……6′
.files\image177.gif)
.files\image377.gif)
.files\image379.gif)
.files\image377.gif)
.files\image382.gif)
.files\image377.gif)
.files\image384.gif)
.files\image377.gif)
.files\image386.gif)
.files\image377.gif)
.files\image388.gif)
.files\image377.gif)
.files\image377.gif)
(2).files\image374.gif) 可取15,16,18.
可取15,16,18.
.files\image390.gif) 表示胜5场负1场,
表示胜5场负1场,.files\image392.gif) ;………………………………7′
;………………………………7′
.files\image394.gif) 表示胜5场平1场,
表示胜5场平1场,.files\image396.gif) ;………………………………8′
;………………………………8′
.files\image398.gif) 表示6场全胜,
表示6场全胜,.files\image400.gif) .……………………………………………9′
.……………………………………………9′
∴.files\image402.gif) .………………………………………………………………12(
.………………………………………………………………12(
19、解:(1)以.files\image404.gif) 所在直线为
所在直线为.files\image048.gif) 轴,以
轴,以.files\image407.gif) 所在直线为
所在直线为.files\image050.gif) 轴,以
轴,以.files\image410.gif) 所在直线为
所在直线为.files\image188.gif) 轴,建立如图所示的空间直角坐标系,由题意可知
轴,建立如图所示的空间直角坐标系,由题意可知.files\image413.gif) 、
、.files\image415.gif) 、
、.files\image417.gif) ………2′
………2′
.files\image419.gif) 令
令.files\image421.gif)
.files\image423.gif)
.files\image425.gif) 的坐标为
的坐标为.files\image427.gif)
.files\image429.gif)
.files\image431.gif) ,
, .files\image433.gif)
.files\image435.gif)
.files\image437.gif)
.files\image439.gif)
.files\image441.gif)
.files\image443.gif) 而
而.files\image445.gif) ,
,.files\image447.gif)
.files\image449.gif) 是
是.files\image451.gif) 与
与.files\image247.gif) 的公垂线…………………………………………………………4′
的公垂线…………………………………………………………4′
(2)令面.files\image454.gif) 的法向量
的法向量.files\image456.gif) 而
而.files\image458.gif) ,
,.files\image460.gif)
.files\image462.gif) 令
令.files\image464.gif) ,则
,则.files\image466.gif) ,即
,即.files\image468.gif) 而面
而面.files\image470.gif) 的法向量
的法向量.files\image472.gif)
.files\image474.gif) ……6′ ∴二面角
……6′ ∴二面角.files\image476.gif) 的大小为
的大小为.files\image478.gif) .……8′
.……8′
(3).files\image480.gif) 面
面.files\image482.gif) 的法向量为
的法向量为.files\image484.gif)
.files\image486.gif) 到面
到面.files\image488.gif) 的距离为
的距离为
.files\image490.gif) 即
即.files\image251.gif) 到面
到面.files\image488.gif) 的距离为
的距离为.files\image493.gif) .…………12′
.…………12′
20、解:(1)假设存在.files\image261.gif) ,使
,使.files\image263.gif) ,则
,则.files\image495.gif) ,同理可得
,同理可得.files\image497.gif) ,以此类推有
,以此类推有.files\image499.gif) ,这与
,这与.files\image259.gif) 矛盾。则不存在
矛盾。则不存在.files\image261.gif) ,使
,使.files\image263.gif) .……3分
.……3分
(2)∵当.files\image269.gif) 时,
时,.files\image501.gif)
又.files\image503.gif) ,
,.files\image259.gif) ,则
,则.files\image505.gif)
∴.files\image507.gif) 与
与.files\image509.gif) 相反,而
相反,而.files\image511.gif) ,则
,则.files\image513.gif) .以此类推有:
.以此类推有:
.files\image515.gif) ,
,.files\image517.gif) ;……7分
;……7分
(3)∵当.files\image269.gif) 时,
时,.files\image503.gif) ,
,.files\image259.gif) ,则
,则.files\image519.gif)
∴.files\image521.gif) …9分
…9分
∴.files\image523.gif) (
(.files\image269.gif) )……10分
)……10分
∴.files\image526.gif) .……12分
.……12分
.files\image527.gif)
21、解(1)设.files\image529.gif) 则
则.files\image531.gif)
①.files\image533.gif) ②
②.files\image535.gif)
①-②得.files\image537.gif)
.files\image539.gif) ……………………2′
……………………2′
.files\image541.gif) 直线
直线.files\image279.gif) 的方程是
的方程是.files\image544.gif) 整理得
整理得.files\image546.gif) ………………4′
………………4′
(2)联立.files\image548.gif) 解得
解得.files\image550.gif)
设.files\image552.gif)
则.files\image554.gif) 且
且.files\image556.gif) 的方程为
的方程为.files\image558.gif) 与
与.files\image560.gif) 联立消去
联立消去.files\image050.gif) ,整理得
,整理得
.files\image563.gif) ………………………………6′
………………………………6′
.files\image565.gif)
.files\image567.gif)
.files\image569.gif)
.files\image571.gif)
.files\image573.gif) 又
又.files\image575.gif)
.files\image577.gif) …………………………………………8′
…………………………………………8′
(3)直线.files\image305.gif) 的方程为
的方程为.files\image580.gif) ,代入
,代入.files\image560.gif) ,得
,得.files\image583.gif) 即
即
.files\image585.gif) ………………………………………………10′
………………………………………………10′
.files\image587.gif) 三点共线,
三点共线,.files\image589.gif) 三点共线,且
三点共线,且.files\image177.gif) 在抛物线的内部。
在抛物线的内部。
令.files\image307.gif) 为
为.files\image593.gif) 、
、.files\image309.gif) 为
为.files\image596.gif)
故由.files\image317.gif) 可推得
可推得.files\image599.gif)
而.files\image601.gif)
.files\image603.gif)
.files\image605.gif) 同理可得:
同理可得:.files\image607.gif)
.files\image609.gif)
而.files\image599.gif) 得
得.files\image612.gif) ………………………………14′
………………………………14′
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com