
题目列表(包括答案和解析)
【解析】观察三视图知该三棱锥的底面为一直角三角形,右侧面也是一直角三角形.故体积等于![]() .
.
【答案】1
已知 ,(其中
,(其中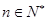 )
)
⑴求 及
及 ;
;
⑵试比较 与
与 的大小,并说明理由.
的大小,并说明理由.
【解析】第一问中取 ,则
,则 ;
…………1分
;
…………1分
对等式两边求导,得
取 ,则
,则 得到结论
得到结论
第二问中,要比较 与
与 的大小,即比较:
的大小,即比较: 与
与 的大小,归纳猜想可得结论当
的大小,归纳猜想可得结论当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时, ;
;
猜想:当 时,
时, 运用数学归纳法证明即可。
运用数学归纳法证明即可。
解:⑴取 ,则
,则 ;
…………1分
;
…………1分
对等式两边求导,得 ,
,
取 ,则
,则 。 …………4分
。 …………4分
⑵要比较 与
与 的大小,即比较:
的大小,即比较: 与
与 的大小,
的大小,
当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时, ;
…………6分
;
…………6分
猜想:当 时,
时, ,下面用数学归纳法证明:
,下面用数学归纳法证明:
由上述过程可知, 时结论成立,
时结论成立,
假设当 时结论成立,即
时结论成立,即 ,
,
当 时,
时,
而
∴
即 时结论也成立,
时结论也成立,
∴当 时,
时, 成立。
…………11分
成立。
…………11分
综上得,当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时,
已知 是公差为d的等差数列,
是公差为d的等差数列, 是公比为q的等比数列
是公比为q的等比数列
(Ⅰ)若  ,是否存在
,是否存在 ,有
,有 ?请说明理由;
?请说明理由;
(Ⅱ)若 (a、q为常数,且aq
(a、q为常数,且aq 0)对任意m存在k,有
0)对任意m存在k,有 ,试求a、q满足的充要条件;
,试求a、q满足的充要条件;
(Ⅲ)若 试确定所有的p,使数列
试确定所有的p,使数列 中存在某个连续p项的和式数列中
中存在某个连续p项的和式数列中 的一项,请证明.
的一项,请证明.
【解析】第一问中,由 得
得 ,整理后,可得
,整理后,可得
 、
、 ,
, 为整数
为整数 不存在
不存在 、
、 ,使等式成立。
,使等式成立。
(2)中当 时,则
时,则
 即
即 ,其中
,其中 是大于等于
是大于等于 的整数
的整数
反之当 时,其中
时,其中 是大于等于
是大于等于 的整数,则
的整数,则 ,
,
显然 ,其中
,其中

 、
、 满足的充要条件是
满足的充要条件是 ,其中
,其中 是大于等于
是大于等于 的整数
的整数
(3)中设 当
当 为偶数时,
为偶数时, 式左边为偶数,右边为奇数,
式左边为偶数,右边为奇数,
当 为偶数时,
为偶数时, 式不成立。由
式不成立。由 式得
式得 ,整理
,整理
当 时,符合题意。当
时,符合题意。当 ,
, 为奇数时,
为奇数时,
结合二项式定理得到结论。
解(1)由 得
得 ,整理后,可得
,整理后,可得
 、
、 ,
, 为整数
为整数 不存在
不存在 、
、 ,使等式成立。
,使等式成立。
(2)当 时,则
时,则
 即
即 ,其中
,其中 是大于等于
是大于等于 的整数反之当
的整数反之当 时,其中
时,其中 是大于等于
是大于等于 的整数,则
的整数,则 ,
,
显然 ,其中
,其中

 、
、 满足的充要条件是
满足的充要条件是 ,其中
,其中 是大于等于
是大于等于 的整数
的整数
(3)设 当
当 为偶数时,
为偶数时, 式左边为偶数,右边为奇数,
式左边为偶数,右边为奇数,
当 为偶数时,
为偶数时, 式不成立。由
式不成立。由 式得
式得 ,整理
,整理
当 时,符合题意。当
时,符合题意。当 ,
, 为奇数时,
为奇数时,

 由
由 ,得
,得

 当
当 为奇数时,此时,一定有
为奇数时,此时,一定有 和
和 使上式一定成立。
使上式一定成立。 当
当 为奇数时,命题都成立
为奇数时,命题都成立
数列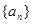 ,满足
,满足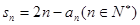
(1)求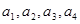 ,并猜想通项公式
,并猜想通项公式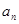 。
。
(2)用数学归纳法证明(1)中的猜想。
【解析】本试题主要考查了数列的通项公式求解,并用数学归纳法加以证明。第一问利用递推关系式得到 ,
,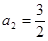 ,
,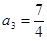 ,
,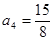 ,并猜想通项公式
,并猜想通项公式
第二问中,用数学归纳法证明(1)中的猜想。
①对n=1, 等式成立。
等式成立。
②假设n=k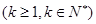 时,
时,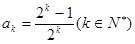 成立,
成立,
那么当n=k+1时,
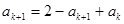 ,所以当n=k+1时结论成立可证。
,所以当n=k+1时结论成立可证。
数列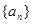 ,满足
,满足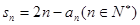
(1) ,
,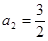 ,
,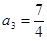 ,
,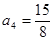 并猜想通项公
并猜想通项公 。 …4分
。 …4分
(2)用数学归纳法证明(1)中的猜想。①对n=1, 等式成立。 …5分
等式成立。 …5分
②假设n=k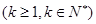 时,
时,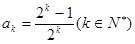 成立,
成立,
那么当n=k+1时,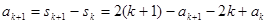
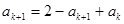 ,
……9分
,
……9分
所以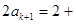
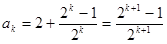
所以当n=k+1时结论成立 ……11分
由①②知,猜想对一切自然数n 均成立
均成立
有以下三个不等式:
 ;
;
 ;
;
 .
.
请你观察这三个不等式,猜想出一个一般性的结论,并证明你的结论。
【解析】根据已知条件可知归纳猜想结论为
下面给出运用综合法的思想求解和证明。解:结论为: . …………………5分
. …………………5分
证明:

所以
1. 构造向量 ,
, ,所以
,所以 ,
, .由数量积的性质
.由数量积的性质 ,得
,得 ,即
,即 的最大值为2.
的最大值为2.
2. ∵ ,令
,令 得
得 ,所以
,所以 ,当
,当 时,
时, ,当
,当 时,
时, ,所以当
,所以当 时,
时, .
.
3.∵ ,∴
,∴ ,
, ,又
,又 ,∴
,∴ ,则
,则 ,所以周期
,所以周期 .作出
.作出 在
在 上的图象知:若
上的图象知:若 ,满足条件的
,满足条件的 (
( )存在,且
)存在,且 ,
, 关于直线
关于直线 对称,
对称, ,
, 关于直线
关于直线 对称,∴
对称,∴ ;若
;若 ,满足条件的
,满足条件的 (
( )存在,且
)存在,且 ,
, 关于直线
关于直线 对称,
对称, ,
, 关于直线
关于直线 对称,
对称,
 ∴
∴ .
.
4. 不等式 (
( )表示的区域是如图所示的菱形的内部,
)表示的区域是如图所示的菱形的内部,
∵
 ,
,
当 ,点
,点 到点
到点 的距离最大,此时
的距离最大,此时 的最大值为
的最大值为 ;
;
当 ,点
,点 到点
到点 的距离最大,此时
的距离最大,此时 的最大值为3.
的最大值为3.
5. 由于已有两人分别抽到5和14两张卡片,则另外两人只需从剩下的18张卡片中抽取,共有 种情况.抽到5 和14的两人在同一组,有两种情况:
种情况.抽到5 和14的两人在同一组,有两种情况:
(1) 5 和14 为较小两数,则另两人需从15~20这6张中各抽1张,有 种情况;
种情况;
(2) 5 和14 为较大两数,则另两人需从1~4这4张中各抽1张,有 种情况.
种情况.
于是,抽到5 和14 两张卡片的两人在同一组的概率为 .
.
 6. ∵
6. ∵ ,∴
,∴ ,
,
设 ,
, ,则
,则 .
.
作出该不等式组表示的平面区域(图中的阴影部分 ).
).
令 ,则
,则 ,它表示斜率为
,它表示斜率为 的一组平行直线,易知,当它经过点
的一组平行直线,易知,当它经过点 时,
时, 取得最小值.
取得最小值.
解方程组 ,得
,得 ,∴
,∴
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com