
题目列表(包括答案和解析)
.有一段演绎推理:“直线平行于平面,则平行于平面内所有直线;已知直线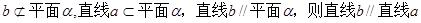 ”。这个结论显然是错误的,这是因为( )
”。这个结论显然是错误的,这是因为( )
A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误
有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线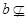 平面
平面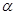 ,直线
,直线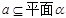 ,直线
,直线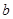 ∥平面
∥平面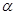 ,则直线
,则直线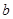 ∥直线
∥直线 ”的结论显然是错误的,这是因为
( )
”的结论显然是错误的,这是因为
( )
A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误
有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线
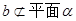 ,直线
,直线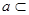 平面
平面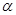 ,直线
,直线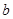 ∥平面
∥平面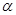 ,则直线
,则直线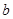 ∥直线
∥直线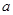 ”的结论显然是错误的,这是因为
”的结论显然是错误的,这是因为
A.大前提错误 B.小前提错误
C.推理形式错误 D.非以上错误
有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线 平
平
面 ,直线
,直线 平面
平面 ,直线
,直线 ∥平面
∥平面 ,则直线
,则直线 ∥直线
∥直线 ”的结论显然是错误的,这
”的结论显然是错误的,这
是因为( )
A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误
有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线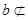 平面
平面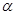 ,直线
,直线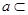 平面
平面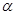 ,直线
,直线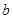 ∥平面
∥平面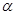 ,则直线
,则直线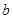 ∥直线
∥直线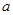 ”的结论显然是错误的,这是因为
”的结论显然是错误的,这是因为
(A)大前提错误 (B)小前提错误 (C)推理形式错误 (D)非以上错误
答题时间:120分钟 满分:150分 命题人:卜阳 校对人:黄雪
一、选择题:(本小题共12题,满分60分)
1、A 2、B 3、B 4、C 5、D 6、C 7、B 8、C 9、A 10、B 11、D 12、A
二、填空题:(本小题共6题,满分30分)
13、14 14、.files/image139.gif) 15、
15、.files/image141.gif) 16、
16、.files/image143.gif) 17、-51 18、240
17、-51 18、240
三、解答题:(本小题共5题,满分60分)
19、(本小题满分12分)
已知复数.files/image111.gif) 满足
满足.files/image113.gif) 为虚数单位),
为虚数单位),.files/image115.gif) ,求一个以
,求一个以.files/image117.gif) 为根的实系数一元二次方程.
为根的实系数一元二次方程.
解: .files/image145.gif) ,
……4分
,
……4分
.files/image147.gif) .
……8分
.
……8分
若实系数一元二次方程有虚根.files/image149.gif) ,则必有共轭虚根
,则必有共轭虚根.files/image151.gif) . ……10分
. ……10分
.files/image153.gif) ,
,
.files/image155.gif) 所求的一个一元二次方程可以是
所求的一个一元二次方程可以是.files/image157.gif) .
……12分
.
……12分
20、(本小题满分12分)
已知:有6个房间安排4个旅游者住,每人可以进住任一房间,且进住房间是等可能的,试求下列各事件的概率:(Ⅰ)事件A:指定的4个房间各有1人;(Ⅱ)事件B:恰有4个房间各有1人;(Ⅲ)事件C:指定的某个房间有2人。
解:由于每人可进住任1房间,进住哪间房是等可能的,每人都有6种等可能的方法,
根据乘法原理,4人进住6个房间共有64种方法
(1)指定的4个房间各有1人,有.files/image159.gif) 种方法,
种方法,.files/image161.gif)
(2)从6间中选出4间有.files/image163.gif) 种方法,4个人每人去1间有
种方法,4个人每人去1间有.files/image159.gif) 种方法,
种方法,.files/image165.gif)
.files/image167.gif)
(3)从4人中选2个人去指定的某个房间,共有.files/image169.gif) 种选法,余下2人每人都可去5个房间中的任1间,因而有52种种方法。
种选法,余下2人每人都可去5个房间中的任1间,因而有52种种方法。.files/image171.gif)
21、(本小题满分12分)
对.files/image119.gif) ,证明:
,证明:.files/image121.gif)
证明:(1)当n=2时,22<.files/image169.gif) =6 < 42; ……2分
=6 < 42; ……2分
(2)假设n=k时,有2 k <.files/image175.gif) < 4 k,
< 4 k,
当n=k+1时,因为.files/image177.gif)
又.files/image179.gif) <4,所以2k+1<
<4,所以2k+1<.files/image181.gif) .
.
所以结论对一切n≥2成立。
22、(本小题满分12分)
若某一等差数列的首项为.files/image123.gif) 展开式中的常数项,其中m是
展开式中的常数项,其中m是.files/image125.gif) -15除以19的余数,则此数列前多少项的和最大?并求出这个最大值。
-15除以19的余数,则此数列前多少项的和最大?并求出这个最大值。
解:由已知得:.files/image183.gif) ……2分
……2分
又.files/image185.gif)
.files/image187.gif) ……5分
……5分
.files/image189.gif) 展开式的通项为
展开式的通项为.files/image191.gif)
.files/image193.gif) 常数项为-4,
常数项为-4,.files/image195.gif) ……8分
……8分
从而等差数列的通项公式是:.files/image197.gif) ……10分
……10分
由.files/image199.gif) 得
得.files/image201.gif)
故此数列的前25项之和与前26项之和相等且最大,.files/image203.gif) 。……12分
。……12分
.files/image205.jpg)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com