
题目列表(包括答案和解析)
已知方向向量为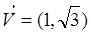 的直线l过椭圆
的直线l过椭圆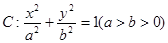 的焦点以及点(0,
的焦点以及点(0,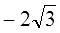 ),直线l与椭圆C交于 A 、B 两点,且A、B两点与另一焦点围成的三角形周长为
),直线l与椭圆C交于 A 、B 两点,且A、B两点与另一焦点围成的三角形周长为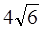 。
。
(1)求椭圆C的方程
(2)过左焦点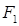 且不与x轴垂直的直线m交椭圆于M、N两点,
且不与x轴垂直的直线m交椭圆于M、N两点,
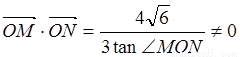 (O坐标原点),求直线m的方程
(O坐标原点),求直线m的方程
已知方向向量为 的直线l过椭圆
的直线l过椭圆 的焦点以及点(0,
的焦点以及点(0, ),直线l与椭圆C交于 A 、B两点,且A、B两点与另一焦点围成的三角形周长为
),直线l与椭圆C交于 A 、B两点,且A、B两点与另一焦点围成的三角形周长为 。
。
(1)求椭圆C的方程
(2)过左焦点 且不与x轴垂直的直线m交椭圆于M、N两点,
且不与x轴垂直的直线m交椭圆于M、N两点, (O坐标原点),求直线m的方程
(O坐标原点),求直线m的方程
已知方向向量为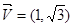 的直线l过椭圆
的直线l过椭圆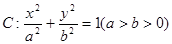 的焦点以及点(0,
的焦点以及点(0,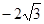 ),直线l与椭圆C交于 A 、B两点,且A、B两点与另一焦点围成的三角形周长为
),直线l与椭圆C交于 A 、B两点,且A、B两点与另一焦点围成的三角形周长为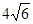 。
。
(1)求椭圆C的方程
(2)过左焦点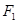 且不与x轴垂直的直线m交椭圆于M、N两点,
且不与x轴垂直的直线m交椭圆于M、N两点,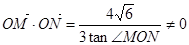 (O坐标原点),求直线m的方程
(O坐标原点),求直线m的方程
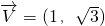 的直线l过椭圆
的直线l过椭圆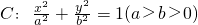 的焦点以及点(0,
的焦点以及点(0,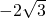 ),直线l与椭圆C交于A、B两点,且A、B两点与另一焦点围成的三角形周长为
),直线l与椭圆C交于A、B两点,且A、B两点与另一焦点围成的三角形周长为 .
.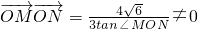 (O坐标原点),求直线m的方程.
(O坐标原点),求直线m的方程.已知方向向量为![]() 的直线l过椭圆
的直线l过椭圆![]() 的焦点以及点(0,
的焦点以及点(0,![]() ),直线l与椭圆C交于 A 、B两点,且A、B两点与另一焦点围成的三角形周长为
),直线l与椭圆C交于 A 、B两点,且A、B两点与另一焦点围成的三角形周长为![]() 。
。
(1)求椭圆C的方程
(2)过左焦点![]() 且不与x轴垂直的直线m交椭圆于M、N两点,
且不与x轴垂直的直线m交椭圆于M、N两点,![]() (O坐标原点),求直线m的方程
(O坐标原点),求直线m的方程
一、
C(B文) CBAA CBBA (D文) B BD
二、
13. 14.-15 15. 16.②③④
三、
17.解:(1)由
得B=2C或2C=
由
B+C>不合题意。
由2C=-B知2C=A+C
ABC为等腰三角形
(2)
又
又
18.解:(1)由
(2)
19.解:(1)密码中同数字的个数为2的事件为密码中只有两个数字,注意到密码的第1,2 列分别总是1,2
(2)
2
3
4
P
(文)解:(1)当且仅当时方程组只有一组解,所以方程组只有一组解的概率
(2)因为方程组只有正数解,所以两直线的交点一定在第一象限,
所以
解得(a,b)可以是(1,4),(1,5),(1,6),(2,1),(2,2),(3,1),(3,2),(4,1),(4,2),(5,1),(5,2,),(6,1),(6,2)
所以
20.(1)
(2)过B作DE的平行线GB交A1A于G,
则
21.解:(1) ①
过原点垂直于I的直线方程 ②
解得①②得
因椭圆中心0(0,0)关于I的对称点在椭圆C的右准线上,
所以
又因为I过椭圆的焦点,所以焦点坐标为(2,0),
所以
故椭圆方程为
(2)当直线m的斜率存在时,得m的方程为代入椭圆方程得
设
点0到m的距离
即
由得
而
即
解得
当m的斜率不存在时,
m的方程为x=-2,也有
且满足
故直线m的方程为
(文))(1)
(2)当m=0时,;
当m>0时,
当m<0时,
22.解:(1)当m=0时,当t<0时,x=0
当 当
(2)因为是偶函数,
所以只要求在[0,1]上的最大值即可,又
①当上为增函数,
所以
故
②当
上为减函数,
所以
故
解得
所以当
当
(3)
(文)解:(1) ①
过原点垂直于I的直线方程为 ②
解①②得
因为椭圆中心0(0,0)关于I的对称点在椭圆C的右准线上,
所以
又因为I过椭圆的焦点,所以焦点坐标为(2,0),
所以
故椭圆方程为
(2)当直线m的斜率存在时,得m的方程为代入椭圆方程得
设
点0到m的距离
即
由得
而
即
解得
当m的斜率不存在时,
m的方程为x=-2,也有
且满足
故直线m的方程为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com