
题目列表(包括答案和解析)
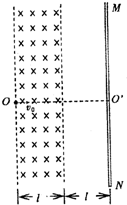 如图所示,MN为一竖直放置足够大的荧光屏,距荧光屏左边l的空间存在着一宽度也为l、方向垂直纸面向里的匀强磁强.O′为荧光屏上的一点,OO′与荧光屏垂直,一质量为m、电荷量为q的带正电的粒子(重力不计)以初速度v0从O点沿OO′方向射入磁场区域.粒子离开磁场后打到荧光屏上时,速度方向与竖直方向成30°角.
如图所示,MN为一竖直放置足够大的荧光屏,距荧光屏左边l的空间存在着一宽度也为l、方向垂直纸面向里的匀强磁强.O′为荧光屏上的一点,OO′与荧光屏垂直,一质量为m、电荷量为q的带正电的粒子(重力不计)以初速度v0从O点沿OO′方向射入磁场区域.粒子离开磁场后打到荧光屏上时,速度方向与竖直方向成30°角.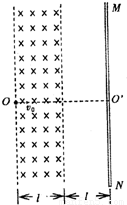
 如图甲所示,MN为一竖直放置的足够大的荧光屏,O为它的中点,OO′与荧光屏垂直,且长度为l.在MN的左侧O′O空间内存在着方向竖直向下的匀强电场,场强大小为E.乙图是从甲图的左侧去看荧光屏得到的平面图,在荧光屏上以O为原点建立如衅乙的直角坐标系.一细束质量为m、电荷为e的电子以相同的初速度v0从O′点O′O方向射入电场区域.电子的重力和电子间的相互作用都可忽略不计.
如图甲所示,MN为一竖直放置的足够大的荧光屏,O为它的中点,OO′与荧光屏垂直,且长度为l.在MN的左侧O′O空间内存在着方向竖直向下的匀强电场,场强大小为E.乙图是从甲图的左侧去看荧光屏得到的平面图,在荧光屏上以O为原点建立如衅乙的直角坐标系.一细束质量为m、电荷为e的电子以相同的初速度v0从O′点O′O方向射入电场区域.电子的重力和电子间的相互作用都可忽略不计.| c |
| d |
| c |
| a |
如图甲所示,MN为一竖直放置的足够大的荧光屏,O为它的中点,OO′与荧光屏垂直,且长度为![]() 。在MN的左侧O′O空间内存在着方向竖直向下的匀强电场,
。在MN的左侧O′O空间内存在着方向竖直向下的匀强电场,
场强大小为E。乙图是从甲图的左侧去看荧光屏得到的平面图,在荧光屏上以O为原点
建立如衅乙的直角坐标系。一细束质量为m、电荷为e的电子以相同的初速度![]() 从O′点O′O方向射入电场区域。电子的重力和电子间的相互作用都可忽略不计。
从O′点O′O方向射入电场区域。电子的重力和电子间的相互作用都可忽略不计。

(1)求电子打在荧光屏上亮点的位置坐标。
(2)若在MN左侧O′O空间内再加一个匀强磁场,使得荧光屏上的亮点恰好位于原点O处,求这个磁场的感应强度B的大小和方向。
(3)如果保持(2)问中磁感应强度不变,但把电场撤去,粒子仍能达到荧光屏上,求荧光屏上的亮点的位置坐标及从O′到荧光屏所需要的时间(若![]() ,则
,则![]() 可用反三角函数表示为
可用反三角函数表示为![]() )。
)。
| L |
| π |
一.选择题(共40分。全部选对得4分,选对但不全的得2分,有选错或不答的得0分。)
题号
1
2
3
4
5
6
7
8
9
10
答案
ABD
ACD
BC
CD
B
A
AC
BC
AC
BC
 二、填空题。(4小题,共20分。)
二、填空题。(4小题,共20分。)
11.(1)连线如图所示(3分)
(2)B C D(3分)
12. (1)辉度 (2)聚焦 (3)垂直位移 水平位移?
(每空1分,共4分)
 |
 (2分)
(2分)14.15:2 (5分)
三、计算题。(4小题,共40分。)
15.解:(1)由图可以读得该交变电流的周期T=0.02 s ………………①
所以,频率f=1/T=50 HZ ………………②
角速度ω=2πf=100π rad/s ………………③
(2)又已知U=10V,R=10Ω,
所以 Um=10 ………………④
………………④
Im= ………………⑤
………………⑤
通过R的电流iR随时间t变化的瞬时表达式为
iR=Imcosωt= cos100πt (A) ………………⑥
cos100πt (A) ………………⑥
评分标准:本题共7分。①、②、③、④、⑤式各1分;⑥式2分。
16.解:(1)导体MN运动时产生的感应电动势  …………①
…………①
R1与R2并联后的电阻为 R并=2R/3 ……………………②
导体MN中的电流为  ……………………③
……………………③
导体棒匀速运动,安培力与拉力平衡, 即有 ……………④
……………④
所以,拉力所做的功为  ……………………⑤
……………………⑤
(2)
流过电阻R1的电流  ……………………⑥
……………………⑥
导体棒移动s所需的时间为  ……………………⑦
……………………⑦
所以,流过电阻R1的电量为  ……………………⑧
……………………⑧
评分标准:本题共8分。①、②、③、④、⑤、⑥、⑦、⑧式各1分。
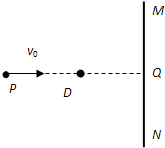
17.解:(1)物体与挡板R碰撞后返回时在磁场中作匀速运动,表明所受洛伦兹力向上与重力平衡。由左手定则可判定物体带负电,进而得知电场的方向向左。
 (2)设物体与挡板R碰撞前后的速度分别为v1、v2,则在物体与挡板R碰撞后的过程里分别有
(2)设物体与挡板R碰撞前后的速度分别为v1、v2,则在物体与挡板R碰撞后的过程里分别有
qv2B=mg ……………………①
 ……………………②
……………………②
由①②解得v2=
B=0.125T……………………④
(3)物体从静止开始运动到与挡板R碰撞前的过程里分别有
 ……………………⑤
……………………⑤
qE=μ(mg+qv1B)……………………⑥
由⑤⑥解得 v1=
物体与挡板碰撞过程中损失的机械能为
 ……………………⑧
……………………⑧
评分标准:本题共12分。每问4分,其中①、②、③、④、⑤、⑥、⑦、⑧式各1分。
 18.解:(1)粒子从O点射入,P点射出,沿直线运动到荧光
18.解:(1)粒子从O点射入,P点射出,沿直线运动到荧光
屏上的S点,如图所示,由几何关系可知,粒子在磁场中
作匀速圆周运动转过的圆心角 ①
①
运动轨道半径为: ②
②
而  ③
③
由②、③解得:B= ④
④
(2)加上电场后,根据运动的独立性,带电粒子沿电场方向匀加速运动,运动加速度为
 ⑤
⑤
粒子在磁场中运动的时间为  ⑥
⑥
则粒子离开复合场时沿电场方向运动速度为  ⑦
⑦
粒子打在荧光屏上时的动能为: ⑧
⑧
评分标准:本题共13分。①、②、③式各1分,④式2分;⑤、⑥、⑦、⑧式各2分。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com