练习册

  • 练习册
  • 试题
    (Ⅲ)解法2:连结FB.因为PC⊥BC.PC⊥AC.且BC∩AC=C.所以PC⊥平面ABC. 即PC是三棱锥P-ABF的高. 【查看更多】

     

    题目列表(包括答案和解析)

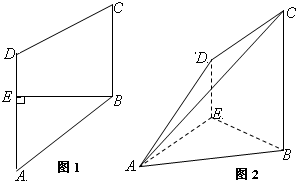    （2013•威海二模）如图1，在梯形ABCD中，BC∥DA，BE⊥DA，EA=EB=BC=2，DE=1，将四边形DEBC沿BE折起，使平面DEBC垂直平面ABE，如图2，连结AD，AC．
    （Ⅰ）若F为AB中点，求证：EF∥平面ADC；
    （Ⅱ）若
    AM
    =λ
    AC
    ，且BM与平面ADC所成角的正弦值为
    2
    		2
    3
    ，试确定点M的位置．

    查看答案和解析>>

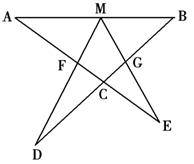
    如图设M为线段AB中点，AE与BD交于点C  ∠DME=∠A=∠B=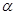，且DM交AC于F，EM交BD于G。

    （1）写出图中三对相似三角形，并对其中一对作出证明；

    （2）连结FG，设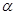=45°，AB=4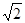，AF=3，求FG长。

     

    查看答案和解析>>

    (理)设x1、x2(x1≠x2)是函数f(x)=ax3+bx2-a2x(a＞0)的两个极值点.

    (1)若x1=-1,x2=2,求函数f(x)的解析式;

    (2)若|x1|+|x2|=,求b的最大值;

    (3)若x1＜x＜x2,且x2=a,函数g(x)=f′(x)-a(x-x1),求证:|g(x)|≤a(3a+2)2.

    (文)如图,N为圆x2+(y-2)2=4上的点,OM为直径,连结MN并延长交x轴于点C,过C引直线垂直于x轴,且与弦ON的延长线交于点D.

    (1)已知点N(,1),求点D的坐标;

    (2)若点N沿着圆周运动,求点D的轨迹E的方程;

    (3)设P(0,a)(a＞0),Q是点P关于原点的对称点,直线l过点P交曲线E于A、B两点,点H在射线QB上,且AH⊥PQ,求证:不论l绕点P怎样转动,恒有.

    查看答案和解析>>

    （选做题）如图设M为线段AB中点，AE与BD交于点C，∠DME=∠A=∠B=α，且DM交AC于F，EM交BD于G。
    （1）写出图中三对相似三角形，并对其中一对作出证明；
    （2）连结FG，设α=45°，AB=4，AF=3，求FG长。

    查看答案和解析>>

    已知直线l:x=my+1过椭圆=1的右焦点F，且交椭圆于A、B两点，点A、B在直线g : x=4上的射影为D、E.

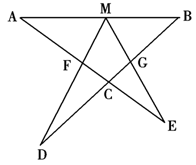
    （1）若直线l交y轴于点M，且=λ1,=λ2,当m变化时，求λ1+λ2的值；

    （2）连结AE、BD，试探索当m变化时，直线AE、BD是否相交于一点是N？若交于定点N，请求出N点的坐标，并给予证明；否则说明理由.

    查看答案和解析>>


    同步练习册答案