
题目列表(包括答案和解析)
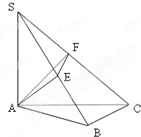 如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程:
如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程:如图 ⊥平面
⊥平面 ,
, ⊥
⊥ ,过
,过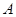 做
做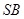
的垂线,垂足为 ,过
,过 做
做 的垂线,垂足为
的垂线,垂足为
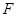 ,求证
,求证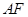 ⊥
⊥ 。以下是证明过程:
。以下是证明过程:
要证
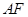 ⊥
⊥
只需证  ⊥平面
⊥平面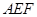
只需证 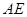 ⊥
⊥ (因为
(因为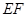 ⊥
⊥ )
)
只需证 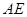 ⊥平面
⊥平面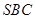
只需证 ① (因为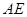 ⊥
⊥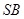 )
)
只需证  ⊥平面
⊥平面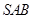
只需证 ② (因为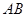 ⊥
⊥ )
)
由只需证 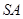 ⊥平面
⊥平面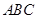 可知上式成立
可知上式成立
所以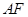 ⊥
⊥
把证明过程补充完整① ②
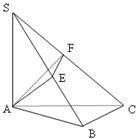

证明:要证AF⊥SC,只需证SC⊥平面AEF,只需证AE⊥SC(因为___________),只需证___________,只需证AE⊥BC(因为___________),只需证BC⊥平面SAB,只需证BC⊥SA(因为___________).由SA⊥平面ABC可知,上式成立.所以,AF⊥SC.
已知曲线 上动点
上动点 到定点
到定点 与定直线
与定直线 的距离之比为常数
的距离之比为常数 .
.
(1)求曲线 的轨迹方程;
的轨迹方程;
(2)若过点 引曲线C的弦AB恰好被点
引曲线C的弦AB恰好被点 平分,求弦AB所在的直线方程;
平分,求弦AB所在的直线方程;
(3)以曲线 的左顶点
的左顶点 为圆心作圆
为圆心作圆 :
: ,设圆
,设圆 与曲线
与曲线 交于点
交于点 与点
与点 ,求
,求 的最小值,并求此时圆
的最小值,并求此时圆 的方程.
的方程.
【解析】第一问利用(1)过点 作直线
作直线 的垂线,垂足为D.
的垂线,垂足为D.
 代入坐标得到
代入坐标得到
第二问当斜率k不存在时,检验得不符合要求;
当直线l的斜率为k时, ;,化简得
;,化简得

第三问点N与点M关于X轴对称,设 ,, 不妨设
,, 不妨设 .
.
由于点M在椭圆C上,所以 .
.
由已知 ,则
,则
 ,
,
由于 ,故当
,故当 时,
时, 取得最小值为
取得最小值为 .
.
计算得, ,故
,故 ,又点
,又点 在圆
在圆 上,代入圆的方程得到
上,代入圆的方程得到 .
.
故圆T的方程为:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com