
题目列表(包括答案和解析)
【解析】如图:|OB|=b,|O F1|=c.∴kPQ=![]() ,kMN=﹣
,kMN=﹣![]() .
.
直线PQ为:y=![]() (x+c),两条渐近线为:y=
(x+c),两条渐近线为:y=![]() x.由
x.由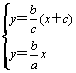 ,得:Q(
,得:Q(![]() ,
,![]() );由
);由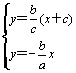 ,得:P(
,得:P(![]() ,
,![]() ).∴直线MN为:y-
).∴直线MN为:y-![]() =﹣
=﹣![]() (x-
(x-![]() ),
),
令y=0得:xM=![]() .又∵|MF2|=|F1F2|=2c,∴3c=xM=
.又∵|MF2|=|F1F2|=2c,∴3c=xM=![]() ,解之得:
,解之得:![]() ,即e=
,即e=![]() .
.
【答案】B
设函数![]() ,
,![]() 则
则![]() 的值域是
的值域是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
【答案】D
设函数![]() ,
,![]() 则
则![]() 的值域是
的值域是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
【答案】D
已知椭圆 (a>b>0),点
(a>b>0),点 在椭圆上。
在椭圆上。
(I)求椭圆的离心率。
(II)设A为椭圆的右顶点,O为坐标原点,若Q在椭圆上且满足|AQ|=|AO|,求直线OQ的斜率的值。
【考点定位】本小题主要考查椭圆的标准方程和几何性质、直线的方程、平面内两点间距离公式等基础知识. 考查用代数方法研究圆锥曲线的性质,以及数形结合的数学思想方法.考查运算求解能力、综合分析和解决问题的能力.
【例】
已知函数y=sin2x+![]() cos2x-2.
cos2x-2.
(1)用“五点法”作出函数在一个周期内的图象;
(2)求这个函数的周期和单调区间;
(3)求函数图象的对称轴方程.
(4)说明图象是由y=sinx的图象经过怎样的变换得到的.
![]() 学科网
学科网
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com