
题目列表(包括答案和解析)
(本小题满分12分) 已知函数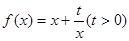 和点
和点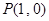 ,过点
,过点 作曲线
作曲线 的两条切线
的两条切线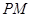 、
、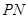 ,切点分别为
,切点分别为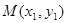 、
、 .
.
(1)求证: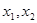 为关于
为关于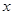 的方程
的方程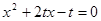 的两根;
的两根;
(2)设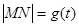 ,求函数
,求函数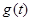 的表达式;
的表达式;
(3)在(2)的条件下,若在区间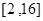 内总存在
内总存在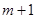 个实数
个实数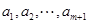 (可以相同),使得不等式
(可以相同),使得不等式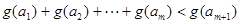 成立,求
成立,求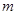 的最大值.
的最大值.
(本小题满分12分)
已知函数 和函数
和函数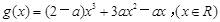
(Ⅰ)令 ,若函数h(x)在[1, +∞)上存在单调递减区间,求实数a的取值范围
,若函数h(x)在[1, +∞)上存在单调递减区间,求实数a的取值范围
(Ⅱ)当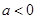 时,若
时,若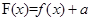 有极大值-7,求实数
有极大值-7,求实数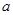 的值.
的值.
(本小题满分12分)
已知函数 和
和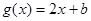 ,若对任意的
,若对任意的 ,恒有
,恒有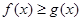
(1) 证明: 且
且
(2) 证明:当 时,
时,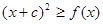
(本小题满分12分)已知函数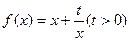 和点
和点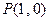 ,过点
,过点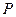 作曲线
作曲线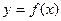 的两条切线
的两条切线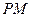 、
、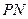 ,切点分别为
,切点分别为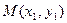 、
、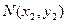 .
.
(1)求证: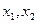 为关于
为关于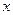 的方程
的方程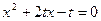 的两根;
的两根;
(2)设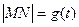 ,求函数
,求函数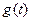 的表达式;
的表达式;
(3)在(2)的条件下,若在区间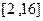 内总存在
内总存在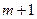 个实数
个实数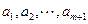 (可以相同),使得不等式
(可以相同),使得不等式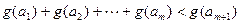 成立,求
成立,求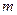 的最大值.
的最大值.
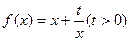 和点
和点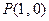 ,过点
,过点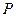 作曲线
作曲线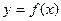 的两条切线
的两条切线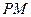 、
、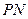 ,切点分别为
,切点分别为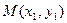 、
、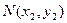 .
.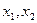 为关于
为关于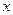 的方程
的方程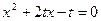 的两根;
的两根; ,求函数
,求函数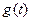 的表达式;
的表达式;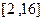 内总存在
内总存在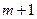 个实数
个实数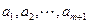 (可以相同),使得不等式
(可以相同),使得不等式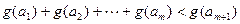 成立,求
成立,求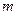 的最大值.
的最大值.
一、选择题
1―5BABAB 6―10DBABA 11―12CC
|