
题目列表(包括答案和解析)
函数![]() 有
有
A.极小值是![]() ,极大值2 ; B.极小值
,极大值2 ; B.极小值![]() ,极大值3;
,极大值3;
C.极小值![]() ,极大值1; D.极小值
,极大值1; D.极小值![]() ,极大值3;
,极大值3;
(选做题)本大题包括A,B,C,D共4小题,请从这4题中选做2小题. 每小题10分,共20分.请在答题卡上准确填涂题目标记. 解答时应写出文字说明、证明过程或演算步骤.
A. 选修4-1:几何证明选讲
 如图,
如图, 是边长为
是边长为 的正方形,以
的正方形,以 为圆心,
为圆心, 为半径的圆弧与以
为半径的圆弧与以 为直径的半⊙O交于点
为直径的半⊙O交于点 ,延长
,延长 交
交 于
于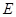 .
.
(1)求证: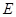 是
是 的中点;(2)求线段
的中点;(2)求线段 的长.
的长.
B.选修4-2:矩阵与变换
已知矩阵A ,其中
,其中 ,若点
,若点 在矩阵A的变换下得到
在矩阵A的变换下得到 .
.
(1)求实数 的值;
的值;
(2)矩阵A的特征值和特征向量.
C. 选修4-4:坐标系与参数方程
在极坐标系中,圆 的极坐标方程为
的极坐标方程为 ,
,
(1)过极点的一条直线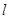 与圆相交于
与圆相交于 ,A两点,且∠
,A两点,且∠ ,求
,求 的长.
的长.
(2)求过圆上一点 ,且与圆相切的直线的极坐标方程;
,且与圆相切的直线的极坐标方程;
D.选修4-5:不等式选讲
已知实数 满足
满足 ,求
,求 的最小值;
的最小值;
(选做题)本大题包括A,B,C,D共4小题,请从这4题中选做2小题. 每小题10分,共20分.请在答题卡上准确填涂题目标记. 解答时应写出文字说明、证明过程或演算步骤.
A. 选修4-1:几何证明选讲
 如图,
如图, 是边长为
是边长为 的正方形,以
的正方形,以 为圆心,
为圆心, 为半径的圆弧与以
为半径的圆弧与以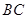 为直径的半⊙O交于点
为直径的半⊙O交于点 ,延长
,延长 交
交 于
于 .
.
(1)求证: 是
是 的中点;(2)求线段
的中点;(2)求线段 的长.
的长.
B.选修4-2:矩阵与变换
已知矩阵A ,其中
,其中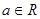 ,若点
,若点 在矩阵A的变换下得到
在矩阵A的变换下得到 .
.
(1)求实数 的值;
的值;
(2)矩阵A的特征值和特征向量.
C. 选修4-4:坐标系与参数方程
在极坐标系中,圆 的极坐标方程为
的极坐标方程为 ,
,
(1)过极点的一条直线 与圆相交于
与圆相交于 ,A两点,且∠
,A两点,且∠ ,求
,求 的长.
的长.
(2)求过圆上一点 ,且与圆相切的直线的极坐标方程;
,且与圆相切的直线的极坐标方程;
D.选修4-5:不等式选讲
已知实数 满足
满足 ,求
,求 的最小值;
的最小值;
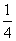 x4+bx2+cx+d,当x=t1时,f(x)有极小值,
x4+bx2+cx+d,当x=t1时,f(x)有极小值,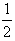 x2+t1x在区间(t1,t2)内最多有一个零点.
x2+t1x在区间(t1,t2)内最多有一个零点. (选做题)本大题包括A,B,C,D共4小题,请从这4题中选做2小题. 每小题10分,共20分.请在答题卡上准确填涂题目标记. 解答时应写出文字说明、证明过程或演算步骤.
 A. 选修4-1:几何证明选讲
A. 选修4-1:几何证明选讲
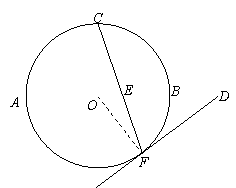
如图,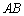 是⊙
是⊙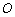 的直径,
的直径,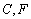 是⊙
是⊙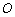 上的两点,
上的两点,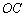 ⊥
⊥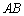 ,
,
过点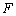 作⊙
作⊙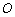 的切线FD交
的切线FD交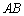 的延长线于点
的延长线于点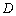 .连结
.连结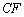 交
交
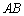 于点
于点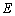 .
.
求证: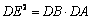 .
.
B. 选修4-2:矩阵与变换
求矩阵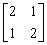 的特征值及对应的特征向量.
的特征值及对应的特征向量.
C. 选修4-4:坐标系与参数方程
已知曲线 的极坐标方程是
的极坐标方程是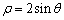 ,直线
,直线 的参数方程是
的参数方程是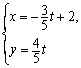 (
(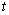 为参数).
为参数).
(1)将曲线 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)设直线 与
与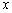 轴的交点是
轴的交点是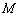 ,
,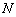 是曲线
是曲线 上一动点,求
上一动点,求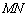 的最大值.
的最大值.
D.选修4-5:不等式选讲
设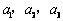 均为正数,且
均为正数,且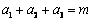 ,求证
,求证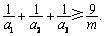
一、选择题:本大题共12小题,每小题5分,共60分,将每小题给出的四个选项中的唯一正确的选项填在答题卡相应的题号中。
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
B
D
A
C
D
A
D
D
A
D
B
|