
题目列表(包括答案和解析)
A.10 B
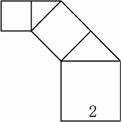
 如图所示是毕达哥拉斯的生长程序:正方形上连接着一个等腰直角三角形,等腰直角三角形的直角边上再连接正方形…,如此继续.若共得到1023个正方形,设起始正方形的边长为
如图所示是毕达哥拉斯的生长程序:正方形上连接着一个等腰直角三角形,等腰直角三角形的直角边上再连接正方形…,如此继续.若共得到1023个正方形,设起始正方形的边长为
| ||
| 2 |
| 1 |
| 32 |
| 1 |
| 32 |
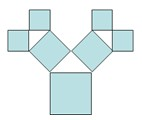
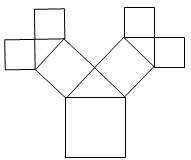 如图所示是毕达哥拉斯的生长程序:正方形一边上连接着等腰直角三角形,等腰直角三角形两直角边再分别连接着一个正方形,如此继续下去,共得到127个正方形.若最后得到的正方形的边长为1,则初始正方形的边长为
如图所示是毕达哥拉斯的生长程序:正方形一边上连接着等腰直角三角形,等腰直角三角形两直角边再分别连接着一个正方形,如此继续下去,共得到127个正方形.若最后得到的正方形的边长为1,则初始正方形的边长为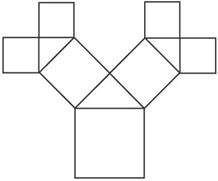
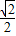 ,则最小正方形的边长为 .
,则最小正方形的边长为 .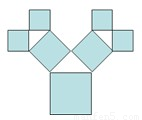
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com