
题目列表(包括答案和解析)
(本题12分)已知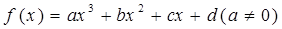 是定义在R上的函数, 且
是定义在R上的函数, 且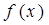 在(-1,0)和(4,5)上有相同的单调性,在(0,2)和(4,5)上
在(-1,0)和(4,5)上有相同的单调性,在(0,2)和(4,5)上
有相反的单调性.
(1) 求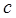 的值;
的值;
(2) 在函数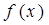 的图象上是否存在一点
的图象上是否存在一点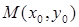 ,使得
,使得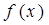 在点
在点 的
的
切线斜率为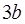 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(本题满分12分)已知函数f(x)=x3+ax2+bx+c,曲线y=f(x)在x=1处的切线![]() 不过第四象限且斜率为3,又坐标原点到切线
不过第四象限且斜率为3,又坐标原点到切线![]() 的距离为
的距离为![]() ,若x=
,若x=![]() 时,y=f(x)有极值.
时,y=f(x)有极值.
(1)求a、b、c的值;w.w.w.k.s.5.u.c.o.m ![]()
![]()
(2)求y=f(x)在[-3,1]上的最大值和最小值.
(本题满分12分)设函数f(x)=x3- ax2+3x+5(a>0).
ax2+3x+5(a>0).
(1)已知f(x)在R上是单调函数,求a的取值范围;
(2)若a=2,且当x∈[1,2]时,f(x)≤m恒成立,求实数m的取值范围.
(本题满分12分)有一枚正方体骰子,六个面分别写1、2、3、4、5、6的数字,规定“抛掷该枚骰子得到的数字是抛掷后,面向上的那一个数字”。已知b和c是先后抛掷该枚骰子得到的数字,函数 =
= 。
。
(Ⅰ)若先抛掷骰子得到的数字是3,求再次抛掷骰子时,使函数 有零点的概率;
有零点的概率;
(Ⅱ) 求函数 在区间(—3,+∞)是增函数的概率
在区间(—3,+∞)是增函数的概率
(本题满分12分)
设f(x)是定义在(0,+∞)上的增函数,且f(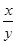 )=f(x)-f(y).[来源:学#科#网]
)=f(x)-f(y).[来源:学#科#网]
(1)求f(1)的值;
(2)若f(6)=1,解不等式f(x+5)-f(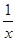 )<2.
)<2.
2008.9
一、(每题5分,共60分)
1.B 2.B 3.B 4.C 5.C 6.A 7.D 8.B 9.A 10.C 11.D 12.B
二、(每题5分,共20分)
13.若 则
则 14.
14.
15.15人 16.20
三、17.(10分)

④当 时,有
时,有
综上所述,m 的取值范围为
……………………………………………………………(10分)
18.(12分)
解:求导得: ,由于
,由于 的图象与直线
的图象与直线




 相切于点(1,-11)所以有
即:
相切于点(1,-11)所以有
即:


……………………………………………………………………………(8分)
解得 ………………………………………………………(10分)
………………………………………………………(10分)
所以 ………………………………………………(12分)
………………………………………………(12分)
19.(12分)
解:(1)当 时,不等式化为:
时,不等式化为: 即
即 …………………(2分)(2)当
…………………(2分)(2)当 时,原不等式可化为:
时,原不等式可化为:
当 时,有
时,有 ∵
∵ ∴
∴ …………(4分)
…………(4分)
当 时,原不等式可化为:
时,原不等式可化为:
①当 即
即 时有
时有
②当 即
即 时
时
③当 即
即 时
时 ………………………………………(10分)
………………………………………(10分)

20.(12分)
解:设剪去的小正方形边长为x┩,则铁盒的底面边长分别为:


 ┩,
┩, ┩,所以有
┩,所以有  得
得 …………(2分)
…………(2分)

设容积为U,则 …………(4分)
…………(4分)
则 令
令 得
得 或
或 (舍去)………(8分)当
(舍去)………(8分)当 时,
时, 当
当 时,
时,
∴当 时,
时, 取得极大值,即
取得极大值,即 的最大值为18………………(11分)
的最大值为18………………(11分)
所以剪去的小正方形边长为1┩时,容积最大,最大容积为18
……………………………………………………………………(12分)
21.(12分)
解:函数 的导数
的导数 令
令 得
得 或
或 ………………………………………………………………(2分)
………………………………………………………………(2分)
当 时,即
时,即 时,函数
时,函数 在
在 上为增函数,不合题意。
上为增函数,不合题意。
……………………………………………………………(4分)
当 时,即
时,即 时,函数
时,函数 在
在 上为增函数,在
上为增函数,在 内为减函数,在
内为减函数,在 上为增函数……………………………………(8分)
上为增函数……………………………………(8分)
依题应有当 时
时 ;当
;当 时
时 所以:
所以: ,解得
,解得 ,因此所求
,因此所求 范围为
范围为 ………………(12分)
………………(12分)
22.(12分)
(Ⅰ)设 ,则
,则 对于
对于 都有
都有
 等价于
等价于 对于
对于 恒成立。………………(2分)
恒成立。………………(2分)
∴只需 在
在 上的最小值
上的最小值 即可
即可
 ∴
∴ 与
与 的关系如下表:
的关系如下表:

-3
(-3,-1)
-1
(-1,2)
2
(2,3)
3

+
0
-
0
+

-45+k
增
7+k
减
-20+k
增
-9+k
于是 的最小值为
的最小值为 ,所以
,所以 ,即
,即 为所求…………………………………………………………………………(6分)
为所求…………………………………………………………………………(6分)
(Ⅱ)对任意 都有“
都有“ ”
”
等价于“ 的最大值小于或等于
的最大值小于或等于 在
在 的最小值”……………………………………………………………………(8分)
的最小值”……………………………………………………………………(8分)
下面求 在
在 上的最小值
上的最小值
列表

-3
(-3,-1)
-1



3

+
0
-
0
+

-21
增
-1
减

增
111
∴ 在
在 上的最小值为-21,又
上的最小值为-21,又 在
在 内最大值为
内最大值为 于是
于是 ∴
∴ 为所求。
为所求。
………………………………………………………………(12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com