
题目列表(包括答案和解析)
设Sn是等比数列{an}的前n项和,对于等比数列{an},有命题P:若S3,S9,S6成等差数列,则a2,a8,a5成等差数列成立;对于命题q:若Sm,Sn,Sl成等差数列,则________成等差数列.请将命题q补充完整,使它也是真命题.(只要一个符合要求的答案即可)
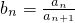 ,是否存在m、k(k>m≥2,k,m∈N*),使得b1、bm、bk成等比数列.若存在,求出所有符合条件的m、k的值;若不存在,请说明理由.
,是否存在m、k(k>m≥2,k,m∈N*),使得b1、bm、bk成等比数列.若存在,求出所有符合条件的m、k的值;若不存在,请说明理由.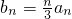 ,求数列bn的前n项和Tn;
,求数列bn的前n项和Tn; ,是否存在m,k(k>m≥2,m,k∈N*),使得b1,bm,bk成等比数列,若存在,求出所有符合条件的m,k的值;若不存在,请说明理由。
,是否存在m,k(k>m≥2,m,k∈N*),使得b1,bm,bk成等比数列,若存在,求出所有符合条件的m,k的值;若不存在,请说明理由。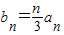 ,求数列bn的前n项和Tn;
,求数列bn的前n项和Tn;1.D 2.C 3.C 4.D 5.A 6.D 7.B 8.C 9.A 10.B
11.B 12.D
13. 14.
14.  15. 11 16.
15. 11 16.

17.(本小题满分12分)
解:(1)
又

(2)
又

18.(本小题满分12分)
解:(1)
∴
∴


(2)∵
∴


 最小正周期为
最小正周期为
由
得
故 的单调递增区间为
的单调递增区间为
19.(本小题满分12分)
解:(1) 成等差数列,
成等差数列,







(2)





20、(本小题满分12分)
(I)解:由 得
得
 ,
,

(II)由 ,
,
∴数列{ }是以S1+1=2为首项,以2为公比的等比数列,
}是以S1+1=2为首项,以2为公比的等比数列,

 当n=1时a1=1满足
当n=1时a1=1满足
(III) ①
①
 ,②
,②
①-②得 ,
,
则 .
.
21、(本小题满分12分) (1)证明:
 (即
(即 的对称轴
的对称轴 )
)



(2)由(1).

经判断: 极小
极小
为0; 
 .
.
22、(本小题满分12分)
解:(1)由椭圆定义及已知条件知2a=|F1B|+|F2B|=10,∴a=5.
又c=4,∴b2=a2-c2=9.
故椭圆方程为 +
+ =1.
=1.
(2)由点B在椭圆上,可知|F2B|=|yB|= ,而椭圆的右准线方程为x=
,而椭圆的右准线方程为x= ,离心率为
,离心率为 ,
,
由椭圆定义有|F2A|= (
( -x1),|F2C|=
-x1),|F2C|= (
( -x2).
-x2).
依题意|F2A|+|F2C|=2|F2B|.
则 (
( -x1)+
-x1)+ (
( -x2)=2×
-x2)=2× .
.
∴x1+x2=8.
设弦AC的中点为P(x0,y0),则x0= =4,
=4,
即弦AC的中点的横坐标为4.
(3)由A(x1,y1),C(x2,y2)在椭圆上得9x12+25y12=9×25,9x22+25y22=9×25.
两式相减整理得9( )+25(
)+25( )(
)( )=0(x1≠x2).
)=0(x1≠x2).
将 =x0=4,
=x0=4, =y0,
=y0, =-
=- (k≠0)代入得
(k≠0)代入得
9×4+25y0(- )=0,即k=
)=0,即k= y0.
y0.
由于P(4,y0)在弦AC的垂直平分线上,
∴y0=4k+m,于是m=y0-4k=y0- y0=-
y0=- y0.
y0.
而- <y0<
<y0< ,∴-
,∴- <m<
<m< .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com