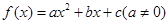设函数，曲线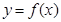通过点(0，2a+3)，且在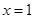处的切线垂直于y轴．

(I)用a分别表示b和c；

(II)当bc取得最大值时，写出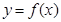的解析式；

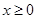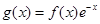(III)在(II)的条件下，若函数g(x)为偶函数,且当时,，求当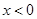时g(x)的表达式，并求函数g(x)在R上的最小值及相应的x值．

 

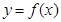设函数，曲线通过点(0，2a+3)，且在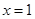处的切线垂直于y轴．

(I)用a分别表示b和c；

(II)当bc取得最大值时，写出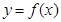的解析式；

(III)在(II)的条件下，g(x)满足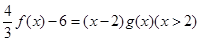，求g(x)的最大值及相应x值．

 

由倍角公式cos2x=2cos²x-1，可知cos2x可以表示为cosx的二次多项式．对于cos3x，我们有
cos3x=cos（2x+x）
=cos2xcosx-sin2xsinx
=（2cos²x-1）cosx-2（sinxcosx）sinx
=2cos³x-cosx-2（1-cos²x）cosx
=4cos³x-3cosx
可见cos3x可以表示为cosx的三次多项式．一般地，存在一个n次多项式P_n（t），使得cosnx=P_n（cosx），这些多项式P_n（t）称为切比雪夫多项式．
（I）求证：sin3x=3sinx-4sin³x；
（II）请求出P₄（t），即用一个cosx的四次多项式来表示cos4x；
（III）利用结论cos3x=4cos³x-3cosx，求出sin18°的值．

某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究，他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数，得到如下资料

日期	3月1日	3月2日	3月3日	3月4日	3月5日
温差x（°C）	10	11	13	12	8
发芽数y（颗）	23	25	30	26	16

（I）从3月1日至3月5日中任选2天，记发芽的种子数分别为m，n，求事件“m，n均小于25”的概率．
（II）请根据3月2日至3月4日的数据，求出y关于x的线性回归方程

y

=

b

x+

a

；
（III）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗，则认为得到的线性回归方程是可靠的，试问（II）所得的线性回归方程是否可靠？