
题目列表(包括答案和解析)
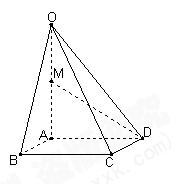
(本小题满分12分)如图,在四棱锥P—ABCD中,侧面PAD是正三角形,且垂直于底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,M为PC上一点,且PA//平面BDM,
(1)求证:M为PC的中点;
(2)求证:面ADM⊥面PBC。

(本小题满分12分)
如图,在四棱锥![]() 中,底面
中,底面![]() 四边长为1的
四边长为1的
菱形,![]() ,
, ![]() ,
, ![]() ,
,
![]() 为
为![]() 的中点.
的中点.
(Ⅰ)求异面直线AB与MD所成角的大小![]() ;
;
(Ⅱ)求点B到平面OCD的距离.
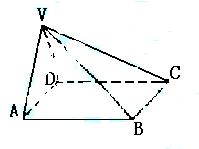
(本小题满分12分)如图,在四棱锥V—ABCD中,底面ABCD是矩形,侧棱VA⊥底面ABCD,E、F、G分别为VA、VB、BC的中点。(I)求证:平面EFG//平面VCD; (II)当二面角V—BC—A、V—DC—A分别为45°、30°时,求直线VB与平面EFG所成的角。
(本小题满分12分)
如图,在四棱锥S—ABCD中,底面ABCD为矩形,SA⊥平面ABCD,二面角S—
CD—A的平面角为![]() ,M为AB中点,N为SC中点.
,M为AB中点,N为SC中点.
(1)证明:MN//平面SAD;
(2)证明:平面SMC⊥平面SCD;
|
(本小题满分12分)如图,在四棱锥![]() 中,底面
中,底面![]() 是正方形,侧面
是正方形,侧面![]() 是正三角形,平面
是正三角形,平面![]() 底面
底面![]() .证明:
.证明:![]() 平面
平面![]() ;
;
一:选择题:BCAAD CCCBA CC
二:填空题:
|