
题目列表(包括答案和解析)
(09年湖北百所重点联考理)(14分)
数列![]()
(1)求证:①![]() ;②
;②![]() ;
;
已知函数![]() .
.
(1)![]()
(2)若![]() 在
在![]() 上单调递增,且在
上单调递增,且在![]() 上单调递减,又满足
上单调递减,又满足![]() 求证:
求证:![]()
(3)在(2)的条件下,若![]() ,试比较
,试比较![]() 的大小,并加以证明。
的大小,并加以证明。
试比较下列各式的大小(不写过程)
(1) 与
与
(2) 与
与
通过上式请你推测出 与
与 且n
且n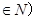 的大小,并用分析法加以证明。
的大小,并用分析法加以证明。
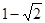 与
与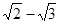
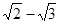 与
与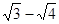
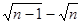 与
与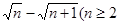 且n
且n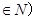 的大小,并用分析法加以证明。
的大小,并用分析法加以证明。已知函数 ,其中常数
,其中常数
(I)若 处取得极值,求a的值;
处取得极值,求a的值;
(II)求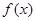 的单调递增区间;
的单调递增区间;
(III)已知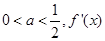 表示
表示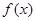 的导数,若
的导数,若 ,
,
且满足 ,试比较
,试比较 的大小,并加以证明。
的大小,并加以证明。
1.D 2.B 3.D 4.B 5.A 6.B 7.C 8.B 9.A 10.C
11..files/image108.gif) 12.
12..files/image110.gif) 13.3 14.
13.3 14..files/image112.gif) 15.①②④
15.①②④
16.解:(1)由题意,得.files/image114.gif) ………………2分
………………2分
解不等式组,得.files/image116.gif) ……4分
……4分
(2).files/image118.gif) ………………6分
………………6分
.files/image120.gif) ………………7分
………………7分
.files/image122.gif)
.files/image124.gif) 上是增函数。 ………………10分
上是增函数。 ………………10分
又.files/image126.gif) ,
,
.files/image128.gif) ………………12分
………………12分
17.解:(1).files/image130.gif) ,
,
.files/image132.gif) 不在集合A中。 ………………3分
不在集合A中。 ………………3分
又.files/image134.gif) , ………………5分
, ………………5分
.files/image136.gif) 上是减函数,
上是减函数,
.files/image138.gif) 在集合A中。 ………………8分
在集合A中。 ………………8分
(2)当.files/image140.gif) , ………………11分
, ………………11分
又由已知.files/image142.gif) ,
,
因此所求的实数k的取值范围是.files/image144.gif) ………………12分
………………12分
18.解:(1)当.files/image146.gif)
.files/image148.gif) ………………2分
………………2分
.files/image150.gif)
.files/image152.gif) , ………………5分
, ………………5分
故.files/image154.gif) ………………6分
………………6分
定义域为.files/image156.gif) ………………7分
………………7分
(2)对于.files/image158.gif) ,
,
显然当.files/image160.gif) (元), ………………9分
(元), ………………9分
.files/image162.gif)
∴当每辆自行车的日租金定在11元时,才能使一日的净收入最多。…………12分
19.解:(1)选取的5只恰好组成完整“奥运吉祥物”的概率
.files/image164.gif) ………………4分
………………4分
(2).files/image166.gif) ………………5分
………………5分
.files/image168.gif)
.files/image170.gif) ………………9分
………………9分
ξ的分布列为
ξ
100
80
60
40
P
.files/image172.gif)
.files/image174.gif)
.files/image176.gif)
.files/image178.gif)
………………11分
.files/image180.gif) ………………13分
………………13分
20.解:(1).files/image182.gif) 恒成立,
恒成立,
知.files/image184.gif)
从而.files/image186.gif) ………………4分
………………4分
(2)由(1)可知.files/image188.gif) ,
,
由于.files/image190.gif) 是单调函数,
是单调函数,
知.files/image192.gif) ………………8分
………………8分
(3).files/image194.gif)
.files/image196.gif) 上是增函数,
上是增函数,
.files/image198.gif)
.files/image200.gif)
………………12分
21.(1)证明:①因为.files/image202.gif)
当且仅当.files/image204.gif)
因为.files/image206.gif) ………………3分
………………3分
②因为.files/image208.gif) ,由①得
,由①得.files/image210.gif) (i)
(i)
下面证明:对于任意.files/image212.gif) 成立。
成立。
.files/image214.gif) 根据(i)、(ii)得
根据(i)、(ii)得.files/image216.gif) ………………9分
………………9分
(2)解:由.files/image218.gif)
从而.files/image220.gif)
因为.files/image222.gif)
………………11分
.files/image224.gif)
当.files/image226.gif)
.files/image228.gif) ………………14分
………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com