
题目列表(包括答案和解析)
命题![]() :
:![]() 是
是![]() 的一条对称轴,
的一条对称轴,![]() :
:![]() 是
是![]() 的最小正周期,有下列命题:①
的最小正周期,有下列命题:①![]() 或
或![]() ;②
;②![]() 且
且![]() ;③非
;③非![]() ;④非
;④非![]() 。其中真命的有( )
。其中真命的有( )
A.0个B.1个C.2个D.3个
命题p: 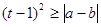 ,其中
,其中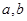 满足条件:五个数
满足条件:五个数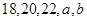 的平均数是20,标准差是
的平均数是20,标准差是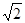 ; 命题q:m≤t≤n ,其中m,n满足条件:点M在椭圆
; 命题q:m≤t≤n ,其中m,n满足条件:点M在椭圆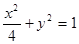 上,定点A(1,0),m、n分别为线段AM长的最小值和最大值。若命题“p或q”为真且命题“p且q”为假,求实数t的取值范围。
上,定点A(1,0),m、n分别为线段AM长的最小值和最大值。若命题“p或q”为真且命题“p且q”为假,求实数t的取值范围。
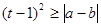 ,其中
,其中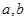 满足条件:五个数
满足条件:五个数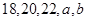 的平均数是20,标准差是
的平均数是20,标准差是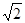 ; 命题q:m≤t≤n ,其中m,n满足条件:点M在椭圆
; 命题q:m≤t≤n ,其中m,n满足条件:点M在椭圆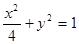 上,定点A(1,0),m、n分别为线段AM长的最小值和最大值。若命题“p或q”为真且命题“p且q”为假,求实数t的取值范围。
上,定点A(1,0),m、n分别为线段AM长的最小值和最大值。若命题“p或q”为真且命题“p且q”为假,求实数t的取值范围。 。
。 p是
p是 q的充分不必要条件,求实数a的取值范围。
q的充分不必要条件,求实数a的取值范围。若p是真命题,q是假命题。以下四个命题 ① p且q ② p或q ③ 非p ④非q。
其中假命题的个数是( )
A.1 B.2 C.3 D.4
一、选择题(本大题共12小题,每小题5分,共60分。
1―5 BBACB 6―10 ADCDD 11―12 AB
二、填空题(本大题共4小题,每小题6分,共16分,
13.14 14.2 15.30 16.①③
三、解答题(本大题共6小题,共计76分)
17.解:(1) …………2分
…………2分

(2)由题设, …………10分
…………10分
 …………12分
…………12分
18.解:(1)记“第一次与第二次取到的球上的号码的和是
 …………5分
…………5分
所以第一次与第二次取到的地球上的号码的和是4的概率 …………6分
…………6分
(2)记“第一次与第二次取到的上的号码的积不小于
 …………11分
…………11分
|