练习册

  • 练习册
  • 试题
    (I)试用表示, 【查看更多】

     

    题目列表(包括答案和解析)

    （1）设a＞0，解关于y的不等式y2-2(
    		a
    +
    1
    		a
    )y+1≤0    ；
    （2）对于任意给定的a≥2，由（1）所确定的y解集（用区间表示）记为I（a），我们规定：区间[m，n]的长度为n-m．如果I（a）的长度为r（a），试求当a取什么值时，r（a）取得最小值，并求r（a）的最小值及此时的I（a）．

    查看答案和解析>>

     

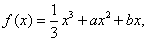    已知函数且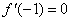

       （I）试用含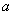的代数式表示；

       （Ⅱ）求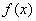的单调区间；                 

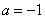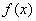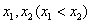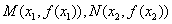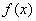       （Ⅲ）令，设函数在处取得极值，记点，证明：线段与曲线存在异于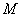、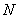的公共点．

     

     

     

     

     

     

    查看答案和解析>>

    （2009•大连二模）（I）已知函数f（x）=x-
    1
    x
    ，x∈(
    1
    4
    ，
    1
    2
    )，P(x1，f(x1))，Q(x2，f(x2))是f(x)    图象上的任意两点，且x1＜x2．
    ①求直线PQ的斜率kPQ的取值范围及f（x）图象上任一点切线的斜率k的取值范围；
    ②由①你得到的结论是：若函数f（x）在[a，b]上有导函数f′（x），且f（a）、f（b）存在，则在（a，b）内至少存在一点ξ，使得f′（ξ）=
    f(b)-f(a)
    b-a
    f(b)-f(a)
    b-a
    成立（用a，b，f（a），f（b）表示，只写出结论，不必证明）
    （II）设函数g（x）的导函数为g′（x），且g′（x）为单调递减函数，g（0）=0．试运用你在②中得到的结论证明：
    当x∈（0，1）时，f（1）x＜g（x）．

    查看答案和解析>>

    设直线与椭圆相切。 （I）试将用表示出来；  （Ⅱ）若经过动点可以向椭圆引两条互相垂直的切线，为坐标原点，求证：为定值。

    查看答案和解析>>

    (本小题满分12分）

    某中学对高二甲、乙两个同类班级进行“加强‘语文阅读理解，训练对提髙‘数学应用题得分率作用”的试验,其中甲班为试验班（加强语文阅读理解训练），乙班为对比班（常规教学,无额外训练），在试验前的测试中，甲、乙两班学生在数学应用题上的得分率基本一致，试验结束后,统计几次数学应用题测试的平均成绩(均取整数)如下表所示：

    60分以下

    61—70 分

    71—80 分

    81-90 分

    91-100分

    甲班(人数）

    3

    6

    11

    18

    12

    乙班(人数）

    8

    13

    15

    10

    现规定平均成绩在80分以上（不含80分）的为优秀.
    (I )试分别估计两个班级的优秀率；

    (II)由以上统计数据填写下面2 X 2列联表，并问是否有"5匁的把握认为“加强‘语文阅读理解’训练对提商‘数学应用题’得分率”有帮助.

    优秀人数

    非优秀人数

    合计

    甲班

    乙班

    合计

    参考公式及数据：，

    0.50

    0.40

    0.25

    0.15

    0.10

    0. 05

    0.025

    0.010

    0.005

    0.001

    K0

    0.455

    0.708

    1.323

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.82

    查看答案和解析>>

    一、选择题：每小题5分，共60分．

           BABDB   DCABD  BD

    二、填空题：本大题共4小题，每小题5分，共20分．把答案填在答题卷相应题号的横线上．

    13．某校有教师200人，男学生1200人，女学生1000人，现用分层抽样的方法从所有老师中抽取一个容量为n的样本；已知从女学生中抽取的人数为80人，则n的值为：16

    14．若△ABC三个内角A、B、C的对边分别是a、b、c，且acosB+bcosA=csinC，则角C的大小为：

    15．若、满足约束条件的最大值为：2

    16．若，且，则实数x的取值范围是：

    三、解答题：本大题共6小题，共70分．把答案填在答题卷相应题号的答题区中．

    17．（本小题满分10分）

    如图，已知，，且，．

    （I）试用表示；

    （Ⅱ）设向量和的夹角为，求的值．

    解：（I）设，则

          ，；            …………3分

    因，，，

           所以         解得：                                                  

           即 ．                                                                                  …………5分

    （Ⅱ）由（I）知 ，又，

    所以 ) ()=，                                     

                                …………8分

    故 ．                                                      …………10分

    18．（本小题满分10分）

    甲、乙等五名奥运志愿者被随机地分配到四个不同的岗位服务，每个岗位至少有一名志愿者．

    （Ⅰ）求甲、乙两人同时被分配到岗位服务的概率；

    （Ⅱ）求甲、乙两人被分配到不同岗位服务的概率．

    解：（Ⅰ）记甲、乙两人同时被分到岗位服务为事件，

    那么，

    即甲、乙两人同时被分到岗位服务的概率是．                                       …………5分

    （Ⅱ）设甲、乙两人同时被分到同一岗位服务为事件，

    那么，

    故甲、乙两人被分到不同岗位服务的概率是．         …………10分

    19．（本小题满分12分）

    如图，四面体ABCD中，O是BD的中点，AB=AD=，CA=CB=CD=BD=2．

    （Ⅰ）求证：AO⊥平面BCD；

    （Ⅱ）求异面直线AB与CD所成角的大小．

     

    解:(方法一)

    （Ⅰ）连结OC．∵BO=DO，AB=AD， BC=CD，

    ∴AO⊥BD，CO⊥BD．                                       …………3分

    在△AOC中，由已知得AC=2，AO=1，CO=，

    ∴AO2+CO2=AC2，∴∠AOC=90°，即AO⊥OC．

     ∴AO平面BCD．           …………6分

    （Ⅱ）分别取AC、BC的中点M、E，连结OM、ME、OE，则

                      ME∥AB，OE∥DC．    

    ∴（或其补角）等于异面直线AB与CD所成的角．                   …………9分

    在△OME中，                                  

    又 是直角△AOC斜边AC上的中线，∴

    ∴

    ∴异面直线AB与CD所成角的大小为                                                …………12分

    (方法二)

    （Ⅰ）同方法一．                                                …………6分

    （Ⅱ）由（Ⅰ）知：AO⊥OC，AO⊥BD，CO⊥BD．

    以O为原点，建立空间直角坐标系如图，  …………7分

    则A(0，0，1)，B(1，0，0)，C(0，，0)，D(-1，0，0) ．     …………10分

    所以 ，

    ∴异面直线AB与CD所成角的大小为                                         …………12分

    20．（本小题满分12分）

    数列满足，且．

       （I）求，并证明数列是等比数列；

       （II）求．

    解：（I），

               ；                       …………2分

      又，，                    …………4分

        且  

        所以数列是以-2为首项，3为公比的等比数列．                   …………6分

       （II）由（I）得，    ．                  …………8分

       

                                   …………10分

                                        …………12分

    21.（本小题满分13分）

    已知函数，在任意一点处的切线的斜率为.

    （I）求函数的单调区间；

    （II）若在上的最小值为，求在R上的极大值.

    21. 解：（I）因,所以；  …………2分

    故  , ，，，

     ,   .                  …………4分

    由知在和上是增函数，

    由知在（-1，2）上为减函数.               …………8分

    （II）由（I）知在（-3，-1）上是增函数，在（-1，2）上为减函数，

    所以 在上的最小值是或，极大值为.       …………10分

    而，,，

    ∴在上的最小值是,∴,.   …………12分

    ，

    即所求函数在R上的极大值为                                 …………13分

    22．（本小题满分13分）

    如图，倾斜角为的直线经过抛物线的焦点F，且与抛物线交于A、B两点．

    （I）求抛物线的焦点F的坐标及准线l的方程；

    （II）若为锐角，作线段AB的垂直平分线m交x轴于点P，证明为定值，并求此定值．

    解：（I）设抛物线的标准方程为，则，从而．

    因此抛物线焦点F的坐标为（2，0），准线方程为．                      ……………4分

    （II）作AC⊥l，BD⊥l，垂足分别为C、D，

    则由抛物线的定义知：|FA|=|AC|，|FB|=|BD|．

    记A、B的横坐标分别为xA、xB，则

    |FA|＝|AC|＝

    解得；                                          ……………7分

    |FB|＝|BD|＝

    解得．                                                                           ……………9分

    记直线m与AB的交点为E，则

    ，

    所以．                                                                  ……………12分

    故．                 ……………13分

     

     

     

     


    同步练习册答案