
题目列表(包括答案和解析)
| C | m n |
| n |
| m |
| C | m-1 n-1 |
| (1+x)[1-(1+x)n] |
| 1-(1+x) |
| (1+x)n+1-(1+x) |
| x |
 ;
;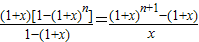 ;,由左边可求得x2的系数为C22+C32+C42+…+Cn2,利用右式可得x2的系数为Cn+13,所以C22+C32+C42+…+Cn2=Cn+13.请利用此方法证明:(C2n)2-(C2n1)2+(C2n2)2-(C2n3)2+…+(C2n2n)2=(-1)nC2nn.
;,由左边可求得x2的系数为C22+C32+C42+…+Cn2,利用右式可得x2的系数为Cn+13,所以C22+C32+C42+…+Cn2=Cn+13.请利用此方法证明:(C2n)2-(C2n1)2+(C2n2)2-(C2n3)2+…+(C2n2n)2=(-1)nC2nn.
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com