
题目列表(包括答案和解析)
某省环保研究所对市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数 与时刻
与时刻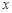 (时) 的关系为
(时) 的关系为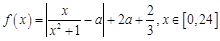 ,其中
,其中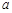 是与气象有关的参数,且
是与气象有关的参数,且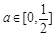 .
.
(1)令 ,
, 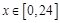 ,写出该函数的单调区间,并选择其中一种情形进行证明;
,写出该函数的单调区间,并选择其中一种情形进行证明;
(2)若用每天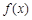 的最大值作为当天的综合放射性污染指数,并记作
的最大值作为当天的综合放射性污染指数,并记作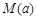 ,求
,求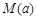 ;
;
(3)省政府规定,每天的综合放射性污染指数不得超过2,试问目前市中心的综合放射性污染指数是否超标?
【解析】第一问利用定义法求证单调性,并判定结论。
第二问(2)由函数的单调性知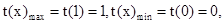 ,
,
∴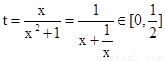 ,即t的取值范围是
,即t的取值范围是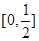 .
.
当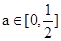 时,记
时,记
则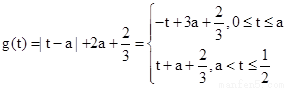
∵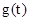 在
在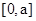 上单调递减,在
上单调递减,在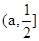 上单调递增,
上单调递增,
第三问因为当且仅当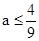 时,
时,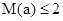 .
.
故当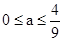 时不超标,当
时不超标,当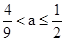 时超标.
时超标.
奖器有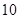 个小球,其中
个小球,其中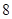 个小球上标有数字
个小球上标有数字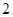 ,
,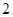 个小球上标有数字
个小球上标有数字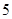 ,现摇出
,现摇出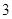 个小球,规定所得奖金(元)为这
个小球,规定所得奖金(元)为这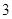 个小球上记号之和,求此次摇奖获得奖金数额的数学期望。
个小球上记号之和,求此次摇奖获得奖金数额的数学期望。
【解析】本试题主要考查了分布列的求解以及运用分布列求解数学期望公式的综合运用。理解随机变量的取值的对应的概率是关键。
P(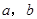 )是平面上的一个点,设事件A表示“
)是平面上的一个点,设事件A表示“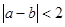 ”,其中
”,其中 为实常数.
为实常数.
(1)若 均为从0,1,2,3,4五个数中任取的一个数,求事件A发生的概率;
均为从0,1,2,3,4五个数中任取的一个数,求事件A发生的概率;
(2)若 均为从区间[0,5)任取的一个数,求事件A发生的概率.
均为从区间[0,5)任取的一个数,求事件A发生的概率.
【解析】本试题考查了几何概型和古典概型结合的一道综合概率计算试题。首先明确区域中的所有基本事件数或者区域表示的面积,然后分别结合概率公式求解得到。
已知函数
 的图像上两相邻最高点的坐标分别为
的图像上两相邻最高点的坐标分别为 和
和 .(Ⅰ)求
.(Ⅰ)求 与
与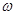 的值;(Ⅱ)在
的值;(Ⅱ)在 中,
中, 分别是角
分别是角 的对边,且
的对边,且 求
求 的取值范围.
的取值范围.
【解析】本试题主要考查了三角函数的图像与性质的综合运用。
第一问中,利用 所以由题意知:
所以由题意知: ,
, ;第二问中,
;第二问中, ,即
,即 ,又
,又 ,
,
则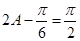 ,解得
,解得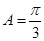 ,
,
所以
结合正弦定理和三角函数值域得到。
解:(Ⅰ) ,
,
所以由题意知: ,
, ;
;
(Ⅱ) ,即
,即 ,又
,又 ,
,
则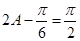 ,解得
,解得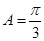 ,
,
所以
因为 ,所以
,所以 ,所以
,所以
(2009全国卷Ⅱ文)(本小题满分12分)
|
|
(Ⅰ)求a,b的值;
(Ⅱ)C上是否存在点P,使得当l绕F转到某一位置时,有![]() 成立?
成立?
若存在,求出所有的P的坐标与l的方程;若不存在,说明理由。
解析:本题考查解析几何与平面向量知识综合运用能力,第一问直接运用点到直线的距离公式以及椭圆有关关系式计算,第二问利用向量坐标关系及方程的思想,借助根与系数关系解决问题,注意特殊情况的处理。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com