
题目列表(包括答案和解析)
【解析】本小题考查直线方程的求法。画草图,由对称性可猜想![]() 。
。
事实上,由截距式可得直线![]() ,直线
,直线![]() ,两式相减得
,两式相减得![]() ,显然直线AB与CP的交点F满足此方程,又原点O也满足此方程,故为所求的直线OF的方程。
,显然直线AB与CP的交点F满足此方程,又原点O也满足此方程,故为所求的直线OF的方程。
答案![]() 。
。
【解析】D.由题得甲队获得冠军有两种情况,第一局胜或第一局输第二局胜,所以甲队获得冠军的概率![]() 所以选D.
所以选D.
【解析】B.由题得三视图对应的直观图是如图所示的直四棱柱,![]()
![]() 。所以选B
。所以选B

【解析】![]() 。由题得
。由题得![]() 所以不等式的解集为
所以不等式的解集为![]() 。
。
已知△ 的内角
的内角 所对的边分别为
所对的边分别为 且
且 .
.
(1)
若 , 求
, 求 的值;
的值;
(2)
若△ 的面积
的面积 求
求 的值.
的值.
【解析】本小题主要考查正弦定理、余弦定理、同角三角函数的基本关系等基础知识,考查运算求解能力。第一问中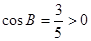 ,得到正弦值
,得到正弦值 ,再结合正弦定理可知,
,再结合正弦定理可知, ,得到
,得到 (2)中
(2)中 即
即 所以c=5,再利用余弦定理
所以c=5,再利用余弦定理 ,得到b的值。
,得到b的值。
解: (1)∵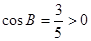 , 且
, 且 , ∴
, ∴  . 由正弦定理得
. 由正弦定理得 , ∴
, ∴ .
.
(2)∵ ∴
∴ . ∴c=5
. ∴c=5
由余弦定理得 ,
,
∴ 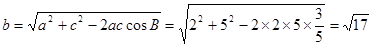
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com