函数y＝Asin（ωx＋φ）（A＞0，ω＞0）在同一周期内，当x＝时，有y_ｍax＝2，当x＝0时，有y_min＝－2?，则函数表达式是　　　　　　　　　　

已知函数y＝Asin(ωx＋φ）(A＞0,ω＞0)在一个周期内，当x＝时，取得最大值2，当x＝时，取得最小值－２，那么（    ）

A.y＝sin（x＋）                 B.y＝２sin（2x＋）

C.y＝２sin（2x＋）                 D.y＝2sin（＋）

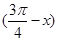当x＝时，函数y＝f(x)＝Asin(x＋φ)(A＞0)取得最小值，则函数y＝f是（    ）

A．奇函数且当x＝时取得最大值     B．偶函数且图象关于点(π，0)对称

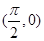C．奇函数且当x＝时取得最小值     D．偶函数且图象关于点对称

当x＝时，函数y＝f(x)＝Asin(x＋φ)(A＞0)取得最小值，则函数y＝f是（   ）

A．奇函数且当x＝时取得最大值	B．偶函数且图象关于点(π，0)对称
C．奇函数且当x＝时取得最小值	D．偶函数且图象关于点对称