C.0.36,64 D.0.36,72——青夏教育精英家教网—

C.0.36,64 D.0.36,72 【查看更多】

在6张卡片上分别写上数字0,1,2,3,4,5,然后把它们混合,再任意排成一行,组成最高位不为0的6位数,则能被5整除的概率为

A.0.2 B.0.3 C.0.36 D.0.46

查看答案和解析>>

某人在比赛（没有“和”局）中赢的概率为0.6，那么他输的概率是（）

A.0.4 B.0.6 C.0.36 D.0.16

查看答案和解析>>

用0、1、2、3四个数字组成允许数字重复的三位数，则这样的三位数共有（　　）

A．64个

B．48个

C．36个

D．16个

查看答案和解析>>

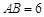设，在线段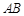上任取两点C,D（端点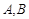除外），将线段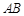分成三条线段AC,CD,DB.

（1）若分成的三条线段的长度均为正整数，求这三条线段可以构成三角形（称事件A）的概率；

（2）若分成的三条线段的长度均为正实数，求这三条线段可以构成三角形（称事件B）的概率；

（3）根据以下用计算机所产生的20组随机数，试用随机数摸拟的方法，来近似计算（Ⅱ）中事件B的概率.

20组随机数如下：

	1组	2组	3组	4组	5组	6组	7组	8组	9组	10组
X	0.52	0.36	0.58	0.73	0.41	0. 6	0.05	0.32	0.38	0.73
Y	0.76	0.39	0.37	0.01	0.04	0.28	0.03	0.15	0.14	0.86

	11组	12组	13组	14组	15组	16组	17组	18组	19组	20组
X	0.67	0.47	0.58	0.21	0.54	0. 64	0.36	0.35	0.95	0.14
Y	0.41	0.54	0.51	0.37	0.31	0.23	0.56	0.89	0.17	0.03

（X是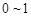之间的均匀随机数，Y也是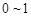之间的均匀随机数）

查看答案和解析>>

用0、1、2、3四个数字组成允许数字重复的三位数，则这样的三位数共有（　　）

A．64个

B．48个

C．36个

D．16个

查看答案和解析>>

一、选择题(本大题共10小题，每小题4分，共40分)

1.B　2.C　3.D　4.C　5.A　6.C　7.B　8.A　9.C　10.A

二、填空题(本大题共4小题，每小题4分，共16分)

11.－4,13

12.75,83

13.203　722　104　088

14.0.2

三、解答题(本大题共3小题，共34分.)

15.(本题满分10分)

解：程序框图如下：

由其他算法得到的程序框图如果合理，请参照上面评分标准给分.

16.(本题满分12分)

解：_甲＝(60＋80＋70＋90＋70)＝74………………………………………………………………2分

_乙＝(80＋60＋70＋80＋75)＝73………………………………………………………………4分

s_甲＝＝＝2………………………………………………………………6分

s_乙＝＝＝2………………………………………………………………8分

∵_甲>_乙，_甲>_乙………………………………………………………………10分

∴甲的平均成绩较好，乙的各门功课发展较平衡………………………………………………………………12分

17.(本题满分12分)

解：(1)分别记白球为1,2,3号，黑球为4,5号.从口袋中每次任取一球，每次取出不放回，连续取两次，其一切可能的结果组成的基本事件(第一次摸到1号，第二次摸到2号球用(1,2)表示)空间为：Ω＝{(1,2)，(2,1)，(1,3)，(3,1)，(1,4)，(4,1)，(1,5)，(5,1)，(2,3)，(3,2)，(2,4)，(4,2)，(2,5)，(5,2)，(3,4)，(4,3)，(3,5)，(5,3),（4,5)，(5,4)}，共有20个基本事件，且上述20个基本事件发生的可能性相同. ………………………………………………………………4分

记“取出的两只球都是白球”为事件A. ………………………………………………………………5分

A＝{(1,2)，(2,1)，(1,3)，(3,1)，(2,3)，(3,2)}，共有6个基本事件. ………………………………………7分

故P(A)＝＝.

所以取出的两只球都是白球的概率为.………………………………………………………………8分

(2)设“取出的两只球中至少有一个白球”为事件B，则其对立事件为“取出的两只球均为黑球”. ………9分

＝{(4,5)，(5,4)}，共有2个基本事件. ………………………………………………………………10分

则P(B)＝1－P()＝1－＝………………………………………………………………11分

所以取出的两只球中至少有一个白球的概率为………………………………………………………………12分

卷二

一、填空题(每小题4分，共16分)

1.1；　2.； 3.；4.6 500

二、解答题(本大题共2小题，共14分)

(本题8分)解：(1)从5张卡片中，任取两张卡片，其一切可能的结果组成的基本事件空间为Ω＝{(0,1)，(0,2)，(0,3)，(0,4)，(1,2)，(1,3)，(1,4)，(2,3)，(2,4)，(3,4)}，共有10个基本事件，且这10个基本事件发生的可能性相同. ……1分

记“两张卡片上的数字之和等于4”为事件A.

A＝{(0,4)，(1,3)}，共有2个基本事件. ………………………………………………………………2分

所以P(A)＝＝………………………………………………………………3分

所以，从中任取两张卡片，两张卡片上的数字之和等于4的概率为…………………………………4分

(2)从5张卡片中，有放回地抽取两次卡片，其一切可能的结果组成的基本事件空间为Ω＝{(x，y)|x∈N，y∈N,0≤x≤4,0≤y≤4}，共有25个基本事件. ……………5分

记“两次取出的卡片上的数字之和恰好等于4”为事件B.

B＝{(0,4)，(4,0)，(1,3)，(3,1)，(2,2)}，共有5个基本事件. ……………6分

则P(B)＝＝……………7分

所以，两次取出的卡片上的数字之和恰好等于4的概率为……………8分

6.(本题6分)

解：(Ⅰ)语句“y＝y＋2”的含义是数列{y_n}，满足y_2n_＋₁＝y_2n_－₁＋2，y₁＝2，

y_{2 009}是以2为公差的等差数列的第1 005项，所以y_{2 009}＝2＋1 004×2＝2 010……………2分

(2)语句“x＝x＋3”和“x＝4x”的含义是

x_n_＋₁＝(k∈N^*)，其中x₁＝4；x_2n_＋₁＝4x_2n＝4(x_2n_－₁＋3) ……………4分

即有x_2n_＋₁＋4＝4(x_2n_－₁＋4)令a_n＝x_2n_－₁＋4，则数列{a_n}是以8为首项，4为公比的等比数列，所以a_n＝8×4ⁿ^－¹＝2×4ⁿ，所以x_2n_＋₁＝2×4ⁿ^＋¹－4

令x_2n_＋₁>2^{2 008}－4，即2×4ⁿ^＋¹－4>2^2
008－4，所以2²ⁿ^＋³>2^{2 008}，所以2n＋3>2 008

即2n＋1>2 006，易知输出框中的“n”即为上述的“2n＋1”

因此输出的n值为2 007. ……………6分

其他正确解法按相应步骤给分.

练习册

高中

初中

小学