练习册

  • 练习册
  • 试题
    无论k为何值时,直线l:kx-y+1+k=0恒过定点 ( )A.(2,1) B C. D. 【查看更多】

     

    题目列表(包括答案和解析)

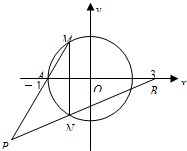
    （2009•湖北模拟）已知A（-1，0）、B（3，0），M、N是圆O：x2+y2=1上的两个动点，且M、N关于x轴对称，直线AM与BN交于P点．
    （1）求P点的轨迹C的方程；
    （2）设动直线l：y=k（x+
    3
    2
    ）与曲线C交于S、T两点．求证：无论k为何值时，以动弦ST为直径的圆总与定直线x=-
    1
    2
    相切．

    查看答案和解析>>

    已知A（-1，0）、B（3，0），M、N是圆O：x2+y2=1上的两个动点，且M、N关于x轴对称，直线AM与BN交于P点．
    （1）求P点的轨迹C的方程；
    （2）设动直线l：y=k（x+）与曲线C交于S、T两点．求证：无论k为何值时，以动弦ST为直径的圆总与定直线x=-相切．

    查看答案和解析>>

    已知A（-1，0）、B（3，0），M、N是圆O：x2+y2=1上的两个动点，且M、N关于x轴对称，直线AM与BN交于P点．
    （1）求P点的轨迹C的方程；
    （2）设动直线l：y=k（x+）与曲线C交于S、T两点．求证：无论k为何值时，以动弦ST为直径的圆总与定直线x=-相切．

    查看答案和解析>>

    已知A（-1，0）、B（3，0），M、N是圆O：x2+y2=1上的两个动点，且M、N关于x轴对称，直线AM与BN交于P点．
    （1）求P点的轨迹C的方程；
    （2）设动直线l：y=k（x+
    3
    2
    ）与曲线C交于S、T两点．求证：无论k为何值时，以动弦ST为直径的圆总与定直线x=-
    1
    2
    相切．
    精英家教网

    查看答案和解析>>

    已知圆C：x2+y2-4x+2y+1=0，直线l：y=kx-1．
    （1）当k为何值时直线l过圆心；
    （2）是否存在直线l与圆C交于A，B两点，且△ABC的面积为2？如果存在，求出直线l的方程，如果不存在，请说明理由；
    （3）设P（x，y）为圆C上一动点，求
    y+3x+1
    的最值．

    查看答案和解析>>

    一、选择题：

    题号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    答案

    B

    A

    B

    C

    B

    A

    B

    C

    B

    A

    A

    D

     

    二、             填空题：（本大题共4小题，每小题5分，共20分．将正确答案填在题中横线上）．

    13.　　　　　c=0　　　　．14.   x-2y+3=0           ．

    15.      16. 

    17.             18.     19.

    20.         21.

    22.

     

     

     

     

     

     

     


    同步练习册答案