
题目列表(包括答案和解析)
 如图:中心为原点的双曲线的一条渐近线为y=x,焦点A、B在x轴上,焦距|AB|为
如图:中心为原点的双曲线的一条渐近线为y=x,焦点A、B在x轴上,焦距|AB|为 .
.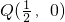 .求证:对于任意直线L,数量积
.求证:对于任意直线L,数量积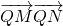 是定值,并求出该定值.
是定值,并求出该定值. .
. .求证:对于任意直线L,数量积
.求证:对于任意直线L,数量积 是定值,并求出该定值.
是定值,并求出该定值.
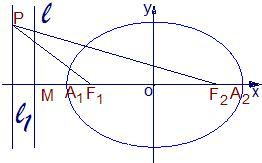 如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|:|A1F1|=2:1.
如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|:|A1F1|=2:1.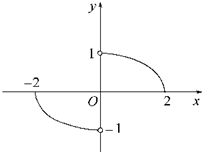 如图,函数y=f(x)的图象是中心在原点、焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )
如图,函数y=f(x)的图象是中心在原点、焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )A、{x|-
| ||||||||
B、{x|-2≤x<-
| ||||||||
C、{x|-2≤x<-
| ||||||||
D、{x|-
|
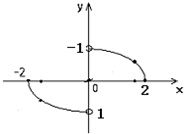 如图,函数y=f(x)的图象是中心在原点,焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )
如图,函数y=f(x)的图象是中心在原点,焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )A、{
| ||||||||
B、{x|-2≤x<
| ||||||||
C、{x|-
| ||||||||
D、{x|-
|
一、选择题(每小题5分,共50分)
1.C 2.B 3.D 4.A 5.C 6.B 7.A 8.C 9.B 10.D
二、填空题(每小题4分.共24分)
11.5
12.4 13.3825 14..files/image303.gif) 15.
15..files/image303.gif) 16.3
16.3
三.解答题(本大题共6小题,共76分)
17.(本题12分)
18.(本题12分]
∵错误!不能通过编辑域代码创建对象。≥.files/image018.gif) ……………………(10分)
……………………(10分)
19.(本题12分)
20.(本题12分)
∴只需 即 …………………………(5分)
∴?=?(-)=2 …………………(9分)
∴?=2.files </div>
</div>
<div class=)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com