题目列表(包括答案和解析)
下面几种推理是类比推理的是 （ ）
A．两条直线平行，同旁内角互补，如果 和 是两条平行直线的同旁内角，则  |
| B．由平面向量的运算性质，推测空间向量的运算性质 |
| C．某校高二级有20个班，1班有51位团员，2班有53位团员，3班有52位团员，由此可以推测各班都超过50位团员,； |
D．一切偶数都能被2整除， 是偶数，所以能被2整除 |
下面几种推理是类比推理的是 （ ）
A．两条直线平行，同旁内角互补，如果
和
是两条平行直线的同旁内角，则 
B．由平面向量的运算性质，推测空间向量的运算性质
C．某校高二级有20个班，1班有51位团员，2班有53位团员，3班有52位团员，由此可以推测各班都超过50位团员,；
D．一切偶数都能被2整除，
是偶数，所以能被2整除
下面几种推理过程是演绎推理的是 ( )
A．两条直线平行，同旁内角互补，如果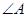
和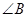
是两条平行直线的同旁内角，则
．
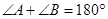B．由平面三角形的性质，推测空间四面体性质．
C．某校高二共有10个班，1班有51人，2班有53人，3班有52人，由此推测各班都超过50人．
D．在数列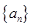
中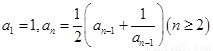
，由此归纳出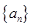的通项公式．
下面几种推理过程是演绎推理的是( )
A．两条直线平行，同旁内角互补，如果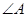
和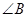
是两条平行直线的同旁内角，则
．
B．由平面三角形的性质，推测空间四面体性质．
C．某校高二共10个班，1班51人，2班53人，3班52人，由此推测各班都超过50人
D．在数列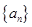
中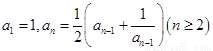
，由此归纳出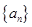的通项公式．
下面几种推理是类比推理的是（ ）
A．两条直线平行，同旁内角互补，如果
和
是两条平行直线的同旁内角，则
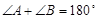
B．由平面向量的运算性质，推测空间向量的运算性质
C．某校高二级有20个班，1班有51位团员，2班有53位团员，3班有52位团员，由此可以推测各班都超过50位团员
D．一切偶数都能被2整除，
是偶数，所以能被2整除
一、选择题（本大题共12小题，每小题4分，共48分）
1．B 2．A 3．D 4．C 5．D 6．C
7．A 8．C 9．B 10．C 11．A 12．B
二、填空题（本大题共4小题，每小题4分，共16分）
13. 
14. 
15. 增函数的定义
16. 与该平面平行的两个平面
三、解答题（本大题共3小题，每小题12分，共36分）
17．（本小题满分12分）
解：（Ⅰ）涉及两个变量，年龄与脂肪含量．
因此选取年龄为自变量
，脂肪含量为因变量
．
作散点图，从图中可看出与具有相关关系．
┄┄┄┄┄┄┄┄┄┄┄┄6分
（Ⅱ）对的回归直线方程为
．
当
时，
，
．
当
时，
，
．
所以
岁和
岁的残差分别为
和
.
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄12分
证明：由于
，
，
所以只需证明
．
展开得
，即
．
所以只需证
．
因为显然成立，
所以
．┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄12分
18B. (本小题满分12分)
证明：（Ⅰ）因为
，所以
．
由于函数
是
上的增函数，
所以
．
同理， 
．
两式相加，得
．┄┄┄┄┄┄┄┄┄┄┄┄6分
（Ⅱ）逆命题：
若，则．
用反证法证明
假设
，那么
所以
．
这与矛盾．故只有，逆命题得证．
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄12分
解：（Ⅰ）由于
，且
．
所以当
时，得
，故
．
从而
．┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄6分
（Ⅱ）数列
不可能为等差数列，证明如下：
由，
得
，
，
．
若存在
，使为等差数列，则
，
即
，解得．
于是
，
．
这与为等差数列矛盾．所以，对任意，数列都不可能是等差数列．
┄┄┄┄┄┄┄┄┄┄┄┄12分
19B. (本小题满分12分)
解：（Ⅰ）
，
．
，
．┄┄┄┄┄┄┄┄┄┄┄6分
（Ⅱ）由（Ⅰ）可得
，
，
．
猜想：
是公比为
的等比数列．
证明如下：因为
，
又
，所以
，
所以数列是首项为
，公比为的等比数列．┄┄┄┄┄┄┄┄┄┄┄┄12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com