
题目列表(包括答案和解析)
设平面向量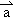 =(
=(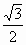 ,-
,- ),
),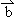 =(
=(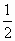 ,
,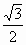 ),若存在不同时为0的两个实数s、t及实数k>0,使
),若存在不同时为0的两个实数s、t及实数k>0,使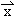 =
=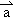 +(t2-k)
+(t2-k)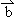 ,
,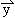 =-s
=-s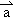 +t
+t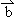 ,且
,且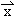 ⊥
⊥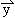 .
.
(1)求函数关系式s=f(t);
(2)若函数s=f(t)在[1,+∞)是单调函数,求证:0<k≤3.
附加题:
(3)设x0≥1,f(x0)≥1,且满足f[f(x0)]=x0,求证f(x0)=x0.
| |||||||||||
设平面上的动向量![]() ,其中s,t为不同时为0的两个实数,实数k≥0,满足
,其中s,t为不同时为0的两个实数,实数k≥0,满足![]()
(1)求函数关系式s=f(t);
(2)若函数f(t)在(1,+∞)上单调递增,求k的范围;
(3)对上述f(t),当k=0时,存在正项数列{an}满足f(a1)+f(a2)+…+f(an)=![]() ,其中Sn=a1+a2+…+an,证明:
,其中Sn=a1+a2+…+an,证明:![]() <3
<3
设平面上的动向量![]() ,其中s,t为不同时为0的两个实数,实数k≥0,满足
,其中s,t为不同时为0的两个实数,实数k≥0,满足![]()
(1)求函数关系式s=f(t);
(2)若函数f(t)在(1,+∞)上单调递增,求k的范围;
(3)对上述f(t),当k=0时,存在正项数列{an}满足f(a1)+f(a2)+…+f(an)=Sn2,其中Sn=a1+a2+…+an,证明:![]() <3
<3
设平面上的动向量![]() ,
,![]() ,其中s、t为不同时为0的两个实数,实数
,其中s、t为不同时为0的两个实数,实数![]() ,满足
,满足![]() 。
。
(1)求函数关系式![]() ;
;
(2)若函数![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的范围;
的范围;
(3)对上述![]() ,当
,当![]() 时,存在正项数列
时,存在正项数列![]() 满足
满足![]() ,其中
,其中![]() ,证明:
,证明: 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com