
题目列表(包括答案和解析)
(本小题满分14分)
某工厂生产一种产品的成本费由三部分组成:
① 职工工资固定支出![]() 元;② 原材料费每件40元;
元;② 原材料费每件40元;
③ 电力与机器保养等费用为每件![]() 元,其中
元,其中![]() 是该厂生产这种产品的总件数.
是该厂生产这种产品的总件数.
(1)把每件产品的成本费![]() (元)表示成产品件数
(元)表示成产品件数![]() 的函数,并求每件产品的最低成本费;
的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量![]() 不超过
不超过![]() 件,且产品能全部销售.根据市场调查:每件产品的销售价
件,且产品能全部销售.根据市场调查:每件产品的销售价![]() 与产品件数
与产品件数![]() 有如下关系:
有如下关系:![]() ,试问生产多少件产品,总利润最高?(总利润=总销售额—总的成本)
,试问生产多少件产品,总利润最高?(总利润=总销售额—总的成本)
(本小题满分14分)我国是水资源比较贫乏的国家之一,各地采用价格调控等手段以达到节约用水的目的.某市用水收费标准是:水费 基本费
基本费 超额费
超额费 定额损耗费,且有如下三条规定:① 若每月用水量不超过最低限量
定额损耗费,且有如下三条规定:① 若每月用水量不超过最低限量 立方米时,只付基本费9元和每户每月定额损耗费
立方米时,只付基本费9元和每户每月定额损耗费 元;② 若每月用水量超过
元;② 若每月用水量超过 立方米时,除了付基本费和定额损耗费外,超过部分每立方米付
立方米时,除了付基本费和定额损耗费外,超过部分每立方米付 元的超额费;③ 每户每月的定额损耗费
元的超额费;③ 每户每月的定额损耗费 不超过5元.
不超过5元.
(1) 求每户每月水费 (元)与月用水量
(元)与月用水量 (立方米)的函数关系;
(立方米)的函数关系;
(2) 该市一家庭今年第一季度每月的用水量和支付 的费用如下表所示:
的费用如下表所示:
| 月份 | 用水量(立方米) | 水费(元) |
| 一 | 4 | 17 |
| 二 | 5 | 23 |
| www.k@s@5@u.com 高#考#资#源#网三 | 2.5 | 11 |
 的值.
的值.(本小题满分14分)某光学仪器厂有一条价值为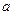 万元的激光器生产线,计划通过技术改造来提高该生产线的生产能力,提高产品的增加值. 经过市场调查,产品的增加值
万元的激光器生产线,计划通过技术改造来提高该生产线的生产能力,提高产品的增加值. 经过市场调查,产品的增加值 万元与技术改造投入
万元与技术改造投入 万元之间满足:①
万元之间满足:① 与
与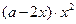 成正比;②当
成正比;②当 时,
时, ,并且技术改造投入满足
,并且技术改造投入满足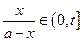 ,其中
,其中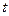 为常数且
为常数且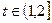 .
.
(I)求 表达式及定义域;
表达式及定义域;
(II)求技术改造之后,产品增加值的最大值及相应 的值.
的值.
(本小题满分14分)
已知函数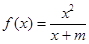 的图像经过点
的图像经过点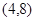 .
.
(1)求该函数的解析式;
(2)数列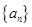 中,若
中,若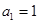 ,
,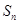 为数列
为数列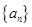 的前
的前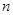 项和,且满足
项和,且满足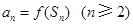 ,
,
证明数列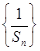 成等差数列,并求数列
成等差数列,并求数列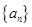 的通项公式;
的通项公式;
(3)另有一新数列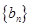 ,若将数列
,若将数列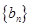 中的所有项按每一行比上一行多一项的规则排成
中的所有项按每一行比上一行多一项的规则排成
如下数表:
|
|
|
|
|
|
|
|
记表中的第一列数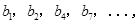 构成的数列即为数列
构成的数列即为数列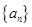 ,上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当
,上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当
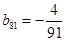 时,求上表中第
时,求上表中第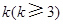 行所有项的和.
行所有项的和.
(本小题满分14分)某工厂生产一种产品的原材料费为每件40元,若用x表示该厂生产这种产品的总件数,则电力与机器保养等费用为每件0.05x元,又该厂职工工资固定支出12500元。
(1)把每件产品的成本费P(x)(元)表示成产品件数x的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量x不超过3000件,且产品能全部销售,根据市场调查:每件产品的销售价Q(x)与产品件数x有如下关系: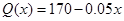 ,试问生产多少件产品,总利润最高?(总利润=总销售额-总的成本)
,试问生产多少件产品,总利润最高?(总利润=总销售额-总的成本)
一、选择题(本大题共8小题,每小题5分,共40分)
1.B 2. C 3. D 4.C 5.B 6.D 7.A 8. B.
二、填空题(本大题共6小题,每小题5分,共30分)
9. ; 10.(-1,2); 11.0; 12.
; 10.(-1,2); 11.0; 12. (或
(或 );
);
 13.(1)
13.(1) 或
或  ;(2)16;(3)
;(2)16;(3) .
.
三、解答题(本大题共6小题,共80分)
14.(本小题满分12分)
解:(Ⅰ)∵

当 时,其图象如右图所示.---4分
时,其图象如右图所示.---4分
(Ⅱ)函数的最小正周期是 ,其单调递增区间是
,其单调递增区间是 ;由图象可以看出,当
;由图象可以看出,当 时,该函数的最大值是
时,该函数的最大值是 .--------------7分
.--------------7分
(Ⅲ)若x是△ABC的一个内角,则有 ,∴
,∴
由 ,得
,得
∴ ∴
∴ ,
, ,故△ABC为直角三角形. --------------12分
,故△ABC为直角三角形. --------------12分
15.(本小题满分12分)
解:(Ⅰ)
 --------6分
--------6分
(Ⅱ)当 时,
时,
 ----------12分
----------12分
16.(本小题满分14分)
 解:(Ⅰ)该几何体的直观图如图1所示,它是有一条
解:(Ⅰ)该几何体的直观图如图1所示,它是有一条
侧棱垂直于底面的四棱锥. 其中底面ABCD是边长为6的
正方形,高为CC1=6,故所求体积是
 ------------------------4分
------------------------4分
 (Ⅱ)依题意,正方体的体积是原四棱锥体积的3倍,
(Ⅱ)依题意,正方体的体积是原四棱锥体积的3倍,
故用3个这样的四棱锥可以拼成一个棱长为6的正方体,
其拼法如图2所示. ------------------------6分
证明:∵面ABCD、面ABB
正方形,于是
 故所拼图形成立.---8分
故所拼图形成立.---8分
 (Ⅲ)方法一:设B1E,BC的延长线交于点G,
(Ⅲ)方法一:设B1E,BC的延长线交于点G,
连结GA,在底面ABC内作BH⊥AG,垂足为H,
连结HB1,则B1H⊥AG,故∠B1HB为平面AB1E与
平面ABC所成二面角或其补角的平面角. --------10分
在Rt△ABG中, ,则
,则
 ,
, ,
,
 ,故平面AB1E与平面ABC所成二面角的余弦值为
,故平面AB1E与平面ABC所成二面角的余弦值为 .---14分
.---14分
方法二:以C为原点,CD、CB、CC1所在直线分别为x、y、z轴建立直角坐标系(如图3),∵正方体棱长为6,则E(0,0,3),B1(0,6,6),A(6,6,0).
设向量n=(x,y,z),满足n⊥ ,n⊥
,n⊥ ,
,
于是 ,解得
,解得 .
--------------------12分
.
--------------------12分
取z=2,得n=(2,-1,2). 又 (0,0,6),
(0,0,6),
故平面AB1E与平面ABC所成二面角的余弦值为 .
----------------14分
.
----------------14分
17.(本小题满分14分)
解:分别记该考生考上第1、2、3批分数线为事件A、B、C,被相应志愿录取为事件Ai、Bi、Ci,(i=a、b), 则以上各事件相互独立. -------------------------------------2分
(Ⅰ)“该考生被第2批b志愿录取”包括上第1批分数线和仅上第2批分数线两种情况,故所求概率为


 . -----------------------------------------------------------------------------------6分
. -----------------------------------------------------------------------------------6分
(Ⅱ)设该考生所报志愿均未录取的概率为 ,则
,则






 .
.
∴该考生能被录取的概率为 . ------------10分
. ------------10分
|