
题目列表(包括答案和解析)
【必做题】(本题满分10分)
某单位举办2010年上海世博会知识宣传活动,进行现场抽奖.盒中装有9张大小相同的精美卡片,卡片上分别印有“世博会会徽”或“海宝”(世博会吉祥物)图案;抽奖规则是:参加者从盒中抽取卡片两张,若抽到两张都是‘‘海宝”,即可获奖,否则,均为不获奖.卡片用后后放同盒子,下一位参加者继续重复进行。
(I)有三人参加抽奖,要使至少一人获奖的概率不低于 ,则“海宝”卡至少多少张?
,则“海宝”卡至少多少张?
(2)若有四张“海宝”卡,现有甲乙丙丁四人依次抽奖.用 表示获奖的人数,求
表示获奖的人数,求 的分布列及E
的分布列及E 的值.
的值.
【必做题】(本题满分10分)
某单位举办2010年上海世博会知识宣传活动,进行现场抽奖.盒中装有9张大小相同的精美卡片,卡片上分别印有“世博会会徽”或“海宝”(世博会吉祥物)图案;抽奖规则是:参加者从盒中抽取卡片两张,若抽到两张都是“海宝”卡即可获奖,否则,均为不获奖.卡片用后放回盒子,下一位参加者继续重复进行.
(I)有三人参加抽奖,要使至少一人获奖的概率不低于![]() ,则“海宝”卡至少多少张?
,则“海宝”卡至少多少张?
(Ⅱ)现有甲乙丙丁四人依次抽奖,用![]() 表示获奖的人数,求
表示获奖的人数,求![]() 的分布列及
的分布列及![]() 的值.
的值.
必做题, 本小题10分.解答时应写出文字说明、证明过程或演算步骤.
某商场搞促销,当顾客购买商品的金额达到一定数量之后可以抽奖,根据顾客购买商品的金额,从箱中(装有4只红球,3只白球,且除颜色外,球的外部特征完全相同)每抽到一只红球奖励20元的商品(当顾客通过抽奖的方法确定了获奖商品后,即将小球全部放回箱中)
(1)当顾客购买金额超过500元而少于1000元(含1000元)时,可从箱中一次随机抽取3个小红球,求其中至少有一个红球的概率;
(2)当顾客购买金额超过1000元时,可一次随机抽取4个小球,设他所获奖商品的金额为 元,求
元,求 的概率分布列和数学期望.
的概率分布列和数学期望.
【必做题】第22题和第23题为必做题, 每小题10分,共20分.要写出必要的文字说明或演算步骤.
有甲、乙两个箱子,甲箱 中有
中有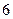 张卡片,其中
张卡片,其中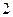 张写有数字
张写有数字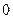 ,
,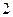 张写有数字
张写有数字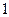 ,
,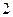 张写有数字
张写有数字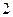 ;乙箱中也有
;乙箱中也有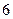 张卡片,其中
张卡片,其中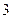 张写有数
张写有数 字
字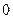 ,
,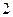 张写有数字
张写有数字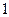 ,
,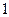 张写有数字
张写有数字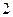 .
.
(1)如果从甲、乙箱中各取一张卡片,设取出的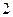 张卡片上数字之积为
张卡片上数字之积为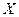 ,求
,求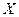 的
的
分布列及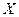 的
的 数学期望;
数学期望;
(2)如果从甲箱中取一张卡片,从乙箱中取两张卡片,那么取出的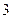 张卡片都写有
张卡片都写有
数字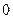 的概率是多少?
的概率是多少?
必做题, 本小题10分.解答时应写出文字说明、证明过程或演算步骤.
某商场搞促销,当顾客购买商品的金额达到一定数量之后可以抽奖,根据顾客购买商品的金额,从箱中(装有4只红球,3只白球,且除颜色外,球的外部特征完全相同)每抽到一只红球奖励20元的商品(当顾客通过抽奖的方法确定了获奖商品后,即将小球全部放回箱中)
(1)当顾客购买金额超过500元而少于1000元(含1000元)时,可从箱中一次随机抽取3个小红球,求其中至少有一个红球的概率;
(2)当顾客购买金额超过1000元时,可一次随机抽取4个小球,设他所获奖商品的金额为 元,求
元,求 的概率分布列和数学期望.
的概率分布列和数学期望.
1. ; 2. 2. 3.200 4. 3 5.
; 2. 2. 3.200 4. 3 5. 6.
6. 7.
7.
8.6 9. ; 10.
; 10. 11.1005 12.4 13. 1 14.
11.1005 12.4 13. 1 14.
 15.解: (1).如图,
15.解: (1).如图, ,
,
即 .
.
(2).在 中,由正弦定理得
中,由正弦定理得

由(1)得 ,
,
即 .
.

16.解:(Ⅰ) 在△PAC中,∵PA=3,AC=4,PC=5,
 ∴
∴ ,∴
,∴ ;又AB=4,PB=5,∴在△PAB中,
;又AB=4,PB=5,∴在△PAB中,
同理可得 
∵ ,∴
,∴
∵ 平面ABC,∴PA⊥BC.
平面ABC,∴PA⊥BC.
(Ⅱ) 如图所示取PC的中点G,
连结AG,BG,∵PF:FC=3:1,∴F为GC的中点
又D、E分别为BC、AC的中点,
∴AG∥EF,BG∥FD,又AG∩GB=G,EF∩FD=F……………7分
∴面ABG∥面DEF
即PC上的中点G为所求的点 …………… 9分
(Ⅲ)
17.解:(1)由题意得 ,
,
整理得 ,解得
,解得 ,
,
所以“学习曲线”的关系式为 .
.
(2)设从第 个单位时间起的2个单位时间内的平均学习效率为
个单位时间起的2个单位时间内的平均学习效率为 ,则
,则

令 ,则
,则 ,
,
显然当 ,即
,即 时,
时, 最大,
最大,
将 代入
代入 ,得
,得 ,
,
所以,在从第3个单位时间起的2个单位时间内的平均学习效率最高.
18. 解:(1)由题可得 ,
, ,设
,设
则 ,
, ,……………………2分
,……………………2分
∴ ,∵点
,∵点 在曲线上,则
在曲线上,则 ,∴
,∴ ,从而
,从而 ,得
,得 .则点P的坐标为
.则点P的坐标为 . ……………………5分
. ……………………5分
(2)由题意知,两直线PA、PB的斜率必存在,设PB的斜率为 ,………6分
,………6分
则BP的直线方程为: .由
.由 得
得
 ,设
,设 ,则
,则 ,
,
 同理可得
同理可得 ,则
,则 ,
, . ………………9分
. ………………9分
所以:AB的斜率 为定值. ………………10分
为定值. ………………10分
(3)设AB的直线方程: .
.
由 ,得
,得 ,
,
由 ,得
,得
P到AB的距离为 ,………………12分
,………………12分
则
 。
。
当且仅当 取等号
取等号
∴三角形PAB面积的最大值为 。………………14分
。………………14分
19.解:
(1)依题意有 ,于是
,于是 .
.
所以数列 是等差数列.
是等差数列.
 .4分
.4分
(2)由题意得 ,即
,即 , (
, ( )
①
)
①
所以又有 .
②
.
②
由② ①得:
①得: , 所以
, 所以 是常数.
是常数.
由 都是等差数列.
都是等差数列.
 ,那么得
,那么得  ,
,
 . (
. (


故
 10分
10分
(3) 当 为奇数时,
为奇数时, ,所以
,所以
当 为偶数时,
为偶数时, 所以
所以
作 轴,垂足为
轴,垂足为 则
则 ,要使等腰三角形
,要使等腰三角形 为正三角形,必须且只须:
为正三角形,必须且只须: .
.
当 为奇数时,有
为奇数时,有 ,即
,即 ①
①
 , 当
, 当 时,.
时,.  不合题意.
不合题意.
当 为偶数时,有
为偶数时,有 ,
, ,同理可求得
,同理可求得  .
.
 ;
; ;当
;当 时,
时, 不合题意.
不合题意.
综上所述,使等腰三角形 中,有正三角形,
中,有正三角形, 的值为
的值为
 ;
; ;
; ;
;
 16分
16分
20⑴当x≥1时, 只需2+a≥0即a≥-2
只需2+a≥0即a≥-2
⑵作差变形可得:

 =
=

 (*)
(*)
 x1>0,x2>o
x1>0,x2>o 

 从而
从而

∴ln ,又a<0 ∴(*)式≥0
,又a<0 ∴(*)式≥0
即 (当且仅当x1=x2时取“=”号)
(当且仅当x1=x2时取“=”号)
 (3)
(3) 可化为:
可化为:
 x
x ∴lnx≤1≤x,因等号不能同时取到,∴lnx<x,lnx―x<0
∴lnx≤1≤x,因等号不能同时取到,∴lnx<x,lnx―x<0
∴a≥
令
 , x
, x ,
,
 =
=
 x
x ,∴lnx―1―
,∴lnx―1― <0,且1―x≤0
<0,且1―x≤0
从而, ,所以g(x)在x
,所以g(x)在x 上递增,从而
上递增,从而 =g(1)= ―
=g(1)= ―
由题设a≥―
即存在x ,不等式f(x)≤(a+3)―
,不等式f(x)≤(a+3)― 能成立且a
能成立且a
21.A解(1)利用△CDO≌△BCM,可证MB=OC= AB
AB
(2)由△PMB∽△BMC,得 ,∴BP=
,∴BP=
B、设M= ,则
,则
 =8
=8 =
= ,故
,故

 =
= ,故
,故
联立以上两方程组解得a=6,b=2,c=4,d=4,故M= .
.
 C.求直线
C.求直线 (
( )被曲线
)被曲线 所截的弦长,将方程
所截的弦长,将方程 ,
, 分别化为普通方程:
分别化为普通方程:
 ,
, ………(5分)
………(5分)
 D.解:由柯西不等式可得
D.解:由柯西不等式可得 


22、解析:(1)记“
 ”为事件A, (
”为事件A, (
 )的取值共有10种情况,…………1分
)的取值共有10种情况,…………1分
满足
 的(
的(
 )的取值有以下4种情况:
)的取值有以下4种情况:
(3,2),(4,2),(5,2),(5,4),
所以 ;
;
(2)随机变量 的取值为2,3,4,5,
的取值为2,3,4,5, 的分布列是
的分布列是

2
3
4
5
P




…………10分
所以 的期望为
的期望为
23、解:(1)由 得
得
∵在数列 中
中 ,∴
,∴ ,∴
,∴
故数列 中的任意一项都小于1
中的任意一项都小于1
(2)由(1)知 ,那么
,那么 ,
,
由此猜想: (n≥2).下面用数学归纳法证明:
(n≥2).下面用数学归纳法证明:
①当n=2时,显然成立;
②当n=k时(k≥2,k∈N)时,假设猜想正确,即 ,
,
那么 ,
,
∴当n=k+1时,猜想也正确
综上所述,对于一切 ,都有
,都有 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com