
题目列表(包括答案和解析)
正方形ABCD的边长为1,点E在边AB上,点F在边BC上,AE=BF=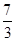 .动点P从E出发沿直线喜爱那个F运动,每当碰到正方形的方向的边时反弹,反弹时反射等于入射角,当点P第一次碰到E时,P与正方形的边碰撞的次数为
.动点P从E出发沿直线喜爱那个F运动,每当碰到正方形的方向的边时反弹,反弹时反射等于入射角,当点P第一次碰到E时,P与正方形的边碰撞的次数为
(A)16(B)14(C)12(D)10
【解析】结合已知中的点E,F的位置,进行作图,推理可知,在反射的过程中,直线是平行的,那么利用平行关系,作图,可以得到回到EA点时,需要碰撞14次即可.
|
关于x1,x2,x3的齐次线性方程组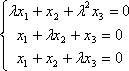 的系数矩阵记为A,且该方程组存在非零解,若存在三阶矩阵B≠O,使得AB=O,(O表示零矩阵,即所有元素均为0的矩阵;|B|表示行列式B的值,该行列式中元素与矩阵B完全相同)则
的系数矩阵记为A,且该方程组存在非零解,若存在三阶矩阵B≠O,使得AB=O,(O表示零矩阵,即所有元素均为0的矩阵;|B|表示行列式B的值,该行列式中元素与矩阵B完全相同)则
A.λ=-2,且|B|=0
B.λ=-2,且|B|≠0
C.λ=1,且|B|≠0
D.λ=1,且|B|=0
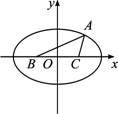
已知B、C是两个定点,|BC|=6,且△ABC的周长等于16,求顶点A的轨迹方程.
探究:在解析几何里,求适合某种条件的点的轨迹方程,要建立适当的坐标系.
如图,由△ABC的周长等于16,|BC|=6可知,点A到B、C两点的距离之和是常数,即|AB|+|AC|=16-6=10,因此,点A的轨迹是以B、C为焦点的椭圆.
已知圆M:![]() 定点
定点![]() ,点P为圆M上的动点,点Q在NP上,点G在MP上,且满足
,点P为圆M上的动点,点Q在NP上,点G在MP上,且满足![]() .
.
(Ⅰ)求点G的轨迹C的方程;
(Ⅱ)过点(2,0)作直线l,与曲线C交于A,B两点,O是坐标原点,设![]() ,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com