练习册

  • 练习册
  • 试题
    在中.两直角边分别为..设为斜边上的高.则.由此类比:三棱锥中的三条侧棱..两两垂直.且长度分别为...设棱锥底面上的高为.则 ． 【查看更多】

     

    题目列表(包括答案和解析)

    ．(2010·深圳市调研)已知函数f(x)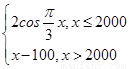＝，则f[f(2010)]＝________.

     

    查看答案和解析>>

    （09年湖北百所重点联考文）（13分）

            某特许专营店销售北京奥运会纪念章，每枚进价为5元，同时每销售一枚这种纪念章还需向北京奥组委交特许经营管理费2元，预计这种纪念章以每枚20元的价格销售时该店一年可销售2000枚，经过市场调研发现每枚纪念章的销售价格在每枚20元的基础上每减少一元则增加销售400枚，而每增加一元则减少销售100枚，现设每枚纪念章的销售价格为x元。

       （1）写出该特许专营店一年内销售这种纪念章所获得的利润y元（y>0）与每枚纪念章的销售价格的函数关系式（并写出这个函数的定义域）；

       （2）当每枚纪念章销售价格x为多少元时，该特许专营店一年内利润y（元）最大，并求出这个最大值。

    查看答案和解析>>

    （09年宜昌一中10月月考文）（13分）

          北京奥运会纪念章某特许专营店销售纪念章，每枚进价为5元，同时每销售一枚这种纪念章还需向北京奥组委交特许经营管理费2元，预计这种纪念章以每枚20元的价格销售时该店一年可销售2000枚，经过市场调研发现每枚纪念章的销售价格在每枚20元的基础上每减少一元则增加销售400枚，而每增加一元则减少销售100枚，现设每枚纪念章的销售价格为元.

    （1）写出该特许专营店一年内销售这种纪念章所获得的利润（元）与每枚纪念章的销售价格的函数关系式（并写出这个函数的定义域）；

    （2）当每枚纪念章销售价格为多少元时，该特许专营店一年内利润（元）最大，并求出这个最大值.

    查看答案和解析>>

    某商店按每件80元的价格，购进商品1000件（卖不出去的商品将成为废品）；市场调研推知：当每件售价为100元时，恰好全部售完；当售价每提高1元时，销售量就减少5件；为获得最大利润，商店决定提高售价x元，获得总利润y元．
    （1）请将y表示为x的函数；
    （2）当售价为多少时，总利润取最大值，并求出此时的利润．

    查看答案和解析>>

    三题中任选两题作答
    （1）（2011年江苏高考）已知矩阵A=
    11
    21
    ，向量β=
    1
    2
    ，求向量α，使得A2α=β
    （2）（2011年山西六校模考）以直角坐标系的原点O为极点，x轴的正半轴为极轴，已知点P的直角坐标为（1，-5），点M的极坐标为(4，
    π
    2
    )    ，若直线l过点P，且倾斜角为
    π
    3
    ，圆C以M为圆心、4为半径．
    ①求直线l的参数方程和圆C的极坐标方程；  ②试判定直线l和圆C的位置关系．
    （3）若正数a，b，c满足a+b+c=1，求
    1
    3a+2
    +
    1
    3b+2
    +
    1
    3c+2
    的最小值．

    查看答案和解析>>


    同步练习册答案