
题目列表(包括答案和解析)
(2006
上海春,20)如图所示,学校科技小组在计算机上模拟航天器变轨返回试验,设计方案如图:航天器运行(按顺时针方向)的轨迹方程为 ,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以y轴为对称轴、
,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以y轴为对称轴、 为顶点的抛物线的实线部分,降落点为D(8,0),观测点A(4,0)、B(6,0)同时跟踪航天器.
为顶点的抛物线的实线部分,降落点为D(8,0),观测点A(4,0)、B(6,0)同时跟踪航天器.
(1)
求航天器变轨后的运行轨迹所在的曲线方程;(2)
试问:当航天器在x轴上方时,观测点A、B测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
(2012年高考上海卷理科21)(6+8=14分)海事救援船对一艘失事船进行定位:以失事船的当前位置为原点,以正北方向为![]() 轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里
轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里![]() 处,如图.现假设:①失事船的移动路径可视为抛物线
处,如图.现假设:①失事船的移动路径可视为抛物线![]() ;②定位后救援船即刻沿直线匀速前往救援;③救援船出发
;②定位后救援船即刻沿直线匀速前往救援;③救援船出发![]() 小时后,失事船所在位置的横坐标为
小时后,失事船所在位置的横坐标为![]() .
.
(1)当![]() 时,写出失事船所在位置
时,写出失事船所在位置![]() 的纵坐标.若此时两船恰好会合,求
的纵坐标.若此时两船恰好会合,求
救援船速度的大小和方向;
(2)问救援船的时速至少是多少海里才能追上失事船?
(本题共2小题,第一小题4分,第二小题8分,共12分)
在学习二项式定理时,我们知道杨辉三角中的数具有两个性质:① 每一行中的二项式系数是“对称”的,即第1项与最后一项的二项式系数相等,第2项与倒数第2项的二项式系数相等,![]() ;② 图中每行两端都是1,而且除1以外的每一个数都等于它肩上两个数的和.我们也知道,性质①对应于组合数的一个性质:
;② 图中每行两端都是1,而且除1以外的每一个数都等于它肩上两个数的和.我们也知道,性质①对应于组合数的一个性质:![]() .
.
(1)试写出性质②所对应的组合数的另一个性质;
(2)请利用组合数的计算公式对(1)中组合数的另一个性质作出证明.
学校科技小组在计算机上模拟航天器变轨返回试验.设计方案如图所示:航天器运行(按顺时针方向)的轨迹方程为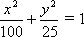
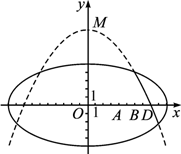
(1)求航天器变轨后的运行轨迹所在的曲线方程; (2)试问:当航天器在x轴上方时,观测点A、B测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
学校科技小组在计算机上模拟航天器变轨返回试验.设计方案如图所示:航天器运行(按顺时针方向)的轨迹方程为![]() +
+![]() =1,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以y轴为对称轴、M(0,
=1,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以y轴为对称轴、M(0,![]() )为顶点的抛物线的实线部分,降落点为D(8,0).观测点A(4,0)、B(6,0)同时跟踪航天器.
)为顶点的抛物线的实线部分,降落点为D(8,0).观测点A(4,0)、B(6,0)同时跟踪航天器.
(1)求航天器变轨后的运行轨迹所在的曲线方程;
(2)试问:当航天器在x轴上方时,观测点A、B测得离航天器距离分别为多少时,向航天器发出变轨指令?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com