
题目列表(包括答案和解析)
(Ⅰ)求证:A1E⊥平面BEP;
(Ⅱ)求直线A1E与平面A1BP所成角的大小;
(Ⅲ)求二面角B-A1P-F的大小(用反三角函数表示)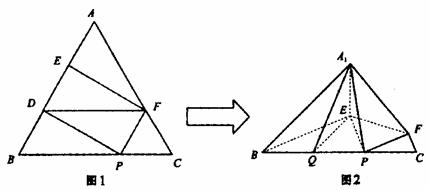
(07年石景山一模文)已知P是双曲线![]() 的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:
的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:
①双曲线的一条准线被它的两条渐近线所截得的线段长度为![]() ;
;
②若|PF1|=e|PF2|,则e的最大值为![]() ;
;
③△PF1F2的内切圆的圆心横坐标为a;
④若直线PF1的斜率为k,则![]()
其中正确命题的序号是 。
已知命题p:函数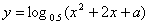 的值域为R,命题q:函数
的值域为R,命题q:函数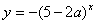 是减函数。若p或q为真命题,p且q为假命题,则实数a的取值范围是( )
是减函数。若p或q为真命题,p且q为假命题,则实数a的取值范围是( )
A.a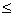 1
B.1<a<2 C.a<2
D.a
1
B.1<a<2 C.a<2
D.a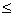 1或a
1或a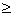 2
2
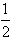 ≤x≤2}且M∩P≠
≤x≤2}且M∩P≠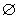 ,求实数a的取值范围;
,求实数a的取值范围;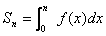 ,是否存在等差数列{an} 和首项为f(1),公比大于0的等比数列{bn},使得a1+a2+…+an+b1+b2+…+bn=Sn?若存在,请求出数列{an}、{bn}的通项公式;若不存在,请说明理由。
,是否存在等差数列{an} 和首项为f(1),公比大于0的等比数列{bn},使得a1+a2+…+an+b1+b2+…+bn=Sn?若存在,请求出数列{an}、{bn}的通项公式;若不存在,请说明理由。己知L1、L2是过点P(-![]() ,0)的两条互相垂直的直线,且L1、L2与双曲线y2-x2=1各有两个交点,且分别为A1、B1和A2、B2。
,0)的两条互相垂直的直线,且L1、L2与双曲线y2-x2=1各有两个交点,且分别为A1、B1和A2、B2。
(1)求L1的斜率k1的取值范围;
(2)若A1恰是双曲线的一个顶点,求|A2B2|的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com