
题目列表(包括答案和解析)
已知函数f(x)=alnx-x2+1.
(1)若曲线y=f(x)在x=1处的切线方程为4x-y+b=0,求实数a和b的值;
(2)若a<0,且对任意x1、x2∈(0,+∞),都|f(x1)-f(x2)|≥|x1-x2|,求a的取值范围.
【解析】第一问中利用f′(x)= -2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0,
-2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0,
由已知得a-2=4,2-a=b,所以a=6,b=-4.
第二问中,利用当a<0时,f′(x)<0,∴f(x)在(0,+∞)上是减函数,
不妨设0<x1≤x2,则|f(x1)-f(x2)|=f(x1)-f(x2),|x1-x2|=x2-x1,
∴|f(x1)-f(x2)|≥|x1-x2|等价于f(x1)-f(x2)≥x2-x1,
即f(x1)+x1≥f(x2)+x2,结合构造函数和导数的知识来解得。
(1)f′(x)= -2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0,
-2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0,
由已知得a-2=4,2-a=b,所以a=6,b=-4.
(2)当a<0时,f′(x)<0,∴f(x)在(0,+∞)上是减函数,
不妨设0<x1≤x2,则|f(x1)-f(x2)|=f(x1)-f(x2),|x1-x2|=x2-x1,
∴|f(x1)-f(x2)|≥|x1-x2|等价于f(x1)-f(x2)≥x2-x1,即f(x1)+x1≥f(x2)+x2,
令g(x)=f(x)+x=alnx-x2+x+1,g(x)在(0,+∞)上是减函数,
∵g′(x)= -2x+1=
-2x+1= (x>0),
(x>0),
∴-2x2+x+a≤0在x>0时恒成立,
∴1+8a≤0,a≤- ,又a<0,
,又a<0,
∴a的取值范围是
求圆心在直线y=-2x上,并且经过点A(2,-1),与直线x+y=1相切的圆的方程.
【解析】利用圆心和半径表示圆的方程,首先
设圆心为S,则KSA=1,∴SA的方程为:y+1=x-2,即y=x-3, ………4分
和y=-2x联立解得x=1,y=-2,即圆心(1,-2)
∴r= =
= ,
,
故所求圆的方程为: +
+ =2
=2
解:法一:
设圆心为S,则KSA=1,∴SA的方程为:y+1=x-2,即y=x-3, ………4分
和y=-2x联立解得x=1,y=-2,即圆心(1,-2) ……………………8分
∴r= =
= ,
………………………10分
,
………………………10分
故所求圆的方程为: +
+ =2
………………………12分
=2
………………………12分
法二:由条件设所求圆的方程为: +
+ =
=
 , ………………………6分
, ………………………6分
解得a=1,b=-2,  =2
………………………10分
=2
………………………10分
所求圆的方程为: +
+ =2
………………………12分
=2
………………………12分
其它方法相应给分
已知函数f(x)(x∈R)满足f(x)= ,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.
,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.
(1)求函数f(x)的表达式;
(2)若数列{an}满足a1= ,an+1=f(an),bn=
,an+1=f(an),bn= -1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;
-1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;
(3)在(2)的条件下,证明:a1b1+a2b2+…+anbn<1(n∈N*).
【解析】解: (1)由f(x)= ,f(1)=1,得a=2b+1.
,f(1)=1,得a=2b+1.
由f(x)=2x只有一解,即 =2x,
=2x,
也就是2ax2-2(1+b)x=0(a≠0)只有一解,
∴b=-1.∴a=-1.故f(x)= .…………………………………………4分
.…………………………………………4分
(2)an+1=f(an)= (n∈N*),bn=
(n∈N*),bn= -1, ∴
-1, ∴ =
= =
= =
= ,
,
∴{bn}为等比数列,q= .又∵a1=
.又∵a1= ,∴b1=
,∴b1= -1=
-1= ,
,
bn=b1qn-1=
 n-1=
n-1= n(n∈N*).……………………………9分
n(n∈N*).……………………………9分
(3)证明:∵anbn=an =1-an=1-
=1-an=1- =
= ,
,
∴a1b1+a2b2+…+anbn= +
+ +…+
+…+ <
< +
+ +…+
+…+
= =1-
=1- <1(n∈N*).
<1(n∈N*).
在△ABC中,a、b、c分别是角A、B、C的对边,cosB= .
.
⑴ 若cosA=- ,求cosC的值; ⑵
若AC=
,求cosC的值; ⑵
若AC= ,BC=5,求△ABC的面积.
,BC=5,求△ABC的面积.
【解析】第一问中sinB=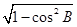 =
= , sinA=
, sinA= =
=
cosC=cos(180°-A-B)=-cos(A+B) =sinA.sinB-cosA·cosB
= ×
× -(-
-(- )×
)× =
=
第二问中,由 =
= +
+ -2AB×BC×cosB得 10=
-2AB×BC×cosB得 10= +25-8AB
+25-8AB
解得AB=5或AB=3综合得△ABC的面积为 或
或
解:⑴ sinB=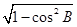 =
= , sinA=
, sinA= =
= ,………………2分
,………………2分
∴cosC=cos(180°-A-B)=-cos(A+B) ……………………3分
=sinA.sinB-cosA·cosB ……………………4分
= ×
× -(-
-(- )×
)× =
= ……………………6分
……………………6分
⑵ 由 =
= +
+ -2AB×BC×cosB得 10=
-2AB×BC×cosB得 10= +25-8AB
………………7分
+25-8AB
………………7分
解得AB=5或AB=3, ……………………9分
若AB=5,则S△ABC= AB×BC×sinB=
AB×BC×sinB= ×5×5×
×5×5× =
= ………………10分
………………10分
若AB=3,则S△ABC= AB×BC×sinB=
AB×BC×sinB= ×5×3×
×5×3× =
= ……………………11分
……………………11分
综合得△ABC的面积为 或
或
已知函数y=x²-3x+c的图像与x恰有两个公共点,则c=
(A)-2或2 (B)-9或3 (C)-1或1 (D)-3或1
【解析】若函数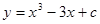 的图象与
的图象与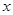 轴恰有两个公共点,则说明函数的两个极值中有一个为0,函数的导数为
轴恰有两个公共点,则说明函数的两个极值中有一个为0,函数的导数为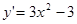 ,令
,令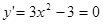 ,解得
,解得 ,可知当极大值为
,可知当极大值为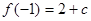 ,极小值为
,极小值为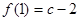 .由
.由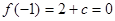 ,解得
,解得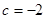 ,由
,由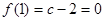 ,解得
,解得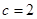 ,所以
,所以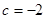 或
或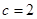 ,选A.
,选A.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com