
题目列表(包括答案和解析)
(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,已知曲线![]() ,将
,将![]() 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的![]() 、2倍后得到曲线
、2倍后得到曲线![]() . 以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
. 以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() .
.
(Ⅰ)试写出直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的参数方程;
的参数方程;
(Ⅱ)在曲线![]() 上求一点P,使点P到直线
上求一点P,使点P到直线![]() 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,已知曲线![]() ,将
,将![]() 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的![]() 、2倍后得到曲线
、2倍后得到曲线![]() . 以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
. 以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() .
.
(Ⅰ)试写出直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的参数方程;
的参数方程;
(Ⅱ)在曲线![]() 上求一点P,使点P到直线
上求一点P,使点P到直线![]() 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
设函数
(1)当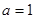 时,求曲线
时,求曲线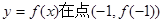 处的切线方程;
处的切线方程;
(2)当 时,求
时,求 的极大值和极小值;
的极大值和极小值;
(3)若函数 在区间
在区间 上是增函数,求实数
上是增函数,求实数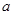 的取值范围.
的取值范围.
【解析】(1)中,先利用 ,表示出点
,表示出点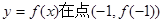 的斜率值
的斜率值 这样可以得到切线方程。(2)中,当
这样可以得到切线方程。(2)中,当 ,再令
,再令 ,利用导数的正负确定单调性,进而得到极值。(3)中,利用函数在给定区间递增,说明了
,利用导数的正负确定单调性,进而得到极值。(3)中,利用函数在给定区间递增,说明了 在区间
在区间 导数恒大于等于零,分离参数求解范围的思想。
导数恒大于等于零,分离参数求解范围的思想。
解:(1)当 ……2分
……2分
 ∴
∴
即 为所求切线方程。………………4分
为所求切线方程。………………4分
(2)当
令 ………………6分
………………6分
∴ 递减,在(3,+
递减,在(3,+ )递增
)递增
∴ 的极大值为
的极大值为 …………8分
…………8分
(3)
①若 上单调递增。∴满足要求。…10分
上单调递增。∴满足要求。…10分
②若
∵ 恒成立,
恒成立,
 恒成立,即a>0……………11分
恒成立,即a>0……………11分
 时,不合题意。综上所述,实数
时,不合题意。综上所述,实数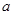 的取值范围是
的取值范围是
选作题,请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分,每道题满分10分)
22、选修4—1:几何证明选讲
如图,△ABC的角平分线AD的延长线交于的外按圆于点E。
(I)证明:△ABC∽△ADC
(II)若△ABC的面积为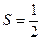 AD·AE,求∠BAC的大小。
AD·AE,求∠BAC的大小。
23、选修4—4:坐标系与参数方程
已知半圆C的参数方程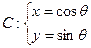
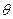 为参数且(0≤
为参数且(0≤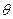 ≤
≤ )
) P为半圆C上一点,A(1,0)O为坐标原点,点M在射线OP上,线段OM与 的长度均为
P为半圆C上一点,A(1,0)O为坐标原点,点M在射线OP上,线段OM与 的长度均为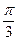 。
。
(I)求以O为极点, 轴为正半轴为极轴建立极坐标系求点M的极坐标。
轴为正半轴为极轴建立极坐标系求点M的极坐标。
(II)求直线AM的参数方程。
24、选修4—5,不等式选讲
已知函数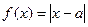
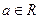
(I)若不等式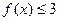 的解集为
的解集为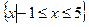 求a值。
求a值。
(II)在(I) 条件下,若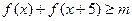 对一切实数
对一切实数 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。
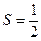 AD·AE,求∠BAC的大小。
AD·AE,求∠BAC的大小。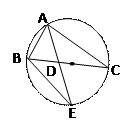
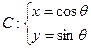
 为参数且(0≤
为参数且(0≤ ≤
≤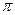 )
)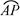 P为半圆C上一点,A(1,0)O为坐标原点,点M在射线OP上,线段OM与 的长度均为
P为半圆C上一点,A(1,0)O为坐标原点,点M在射线OP上,线段OM与 的长度均为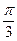 。
。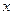 轴为正半轴为极轴建立极坐标系求点M的极坐标。
轴为正半轴为极轴建立极坐标系求点M的极坐标。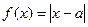
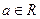
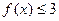 的解集为
的解集为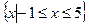 求a值。
求a值。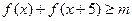 对一切实数
对一切实数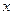 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com