练习册

  • 练习册
  • 试题
    例3.下表是某款车的车速与刹车后停车距离.试分别就三种函数关系建立数学模型.并探讨最佳模拟.根据最佳模拟求车速为时的刹车距离.车速101530405060708090100停车距离(m)471218253443546680 【查看更多】

     

    题目列表(包括答案和解析)

    2009年春季，我国部分地区H1N1流行，党和政府采取果断措施，防治结合，很快使病情得到控制．下表是某同学记载的5月1号到5月12号每天北京市H1N1病治愈者数据，根据这些数据绘制散点图．
    日期 5.1 5.2 5.3 5.4 5.5 5.6
    人数 100 109 115 118 121 134
    日期 5.7 5.8 5.9 5.10 5.11 5.12
    人数 141 152 168 175 186 203
    下列说法正确的个数有（　　）
    ①根据此散点图，可以判断日期与人数具有线性相关关系；
    ②根据此散点图，可以判断日期与人数具有一次函数关系；
    ③后三天治愈出院的人数占这12天治愈出院人数的30%多；
    ④后三天中每天治愈出院的人数均超过这12天内北京市H1N1病愈者总人数的20%．

    查看答案和解析>>

    （2012•武昌区模拟）下表是某机电设备的广告费用x与销售额y的统计数据：
    广告费用x（万元） 2 3 4 5
    销售额y（万元） 54 49 39 26
    根据上表可得回归直线方程
    y
    =
    b
    x+
    a
    中
    a
    为9.1    ，据此模型预报广告费用为6万元时销售额为（　　）

    查看答案和解析>>

    （2012•武汉模拟）下表是某商场统计的20名营业员在某月的销售额（单位：万元）．假设销售额的中位数为a，众数为b，平均值为c，则它们的大小关系为
    b＜a＜c
    b＜a＜c
    ．
    销售额/万元 15 16 17 18 19 22 23 24 26 28
    频数（人数） 4 3 2 2 3 1 1 1 2 1

    查看答案和解析>>

    2003年春季，我国部分地区SARS流行，党和政府采取果断措施，防治结合，很快使病情得到控制，下表是某同学记载的5月1日至5月12日每天北京市SARS治愈者数据，以及根据这些数据绘制出的散点图
    日期 5.1 5.2 5.3 5.4 5.5 5.6 5.7 5.8 5.9 5.10 5.11 5.12
    人数 100 109 115 118 121 134 141 152 168 175 186 203
    下列说法：
    ①根据此散点图，可以判断日期与人数具有线性相关关系；
    ②根据此散点图，可以判断日期与人数具有一次函数关系．
    其中正确的个数为（　　）

    查看答案和解析>>

    2010年，我国部分地区手足口病流行，党和政府采取果断措施防、治结合，很快使病情得到控制．下表是某医院记载的5月1日到5月12日每天治愈者数据及根据数据绘制的散点图.

    日期

    5.1

    5.2

    5.3

    5.4

    5.5

    5.6

    人数

    100

    109

    115

    118

    121

    134

     

     

     

     

     

     

     

    日期

    5.7

    5.8

    5.9

    5.10

    5.11

    5.12

    人数

    141

    152

    168

    175

    186

    203

     

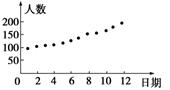
    则下列说法：①根据此散点图，可以判断日期与治愈人数具有线性相关关系；②根据此散点图，可以判断日期与治愈人数具有一次函数关系；③根据此散点图，可以判断日期与治愈人数呈正相关．

    其中正确的有(　　)

    A．0个                           B．1个

    C．2个                           D．3个

     

    查看答案和解析>>


    同步练习册答案