
题目列表(包括答案和解析)
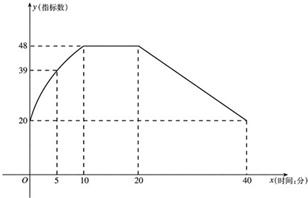 通过实验研究,专家们发现:初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的,讲课开始时,学生的兴趣激增,中间有一段时间,学生的兴趣保持平稳的状态,随后开始分散.学生注意力指标数y随时间x(分钟)变化的函数图象如图所示(y越大表示学生注意力越集中).当0≤x≤10时,图象是抛物线的一部分,当10≤x≤20和20≤x≤40时,图象是线段.
通过实验研究,专家们发现:初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的,讲课开始时,学生的兴趣激增,中间有一段时间,学生的兴趣保持平稳的状态,随后开始分散.学生注意力指标数y随时间x(分钟)变化的函数图象如图所示(y越大表示学生注意力越集中).当0≤x≤10时,图象是抛物线的一部分,当10≤x≤20和20≤x≤40时,图象是线段.| k |
| x |
| x(天) | 10 | 20 | 25 | 30 |
| Q(x)(件) | 110 | 120 | 125 | 120 |
 (2006•静安区二模)某种洗衣机在洗涤衣服时,需经过进水、清洗、排水、脱水四个连续的过程.假设进水时水量匀速增加,清洗时水量保持不变.已知进水时间为4分钟,清洗时间为12分钟,排水时间为2分钟,脱水时间为2分钟.洗衣机中的水量y(升)与时间x(分钟)之间的关系如下表所示:
(2006•静安区二模)某种洗衣机在洗涤衣服时,需经过进水、清洗、排水、脱水四个连续的过程.假设进水时水量匀速增加,清洗时水量保持不变.已知进水时间为4分钟,清洗时间为12分钟,排水时间为2分钟,脱水时间为2分钟.洗衣机中的水量y(升)与时间x(分钟)之间的关系如下表所示:| x | 0 | 2 | 4 | 16 | 16.5 | 17 | 18 | … |
| y | 0 | 20 | 40 | 40 | 29.5 | 20 | 2 | … |
| a |
| x |
| 1 |
| x |
| 1 |
| x2 |
| f(x1)+f(x2) |
| 2 |
| 3 |
| 2 |
| g(x1)+g(x2) |
| 2 |
| 3 |
| 2 |
| lgx1+lgx2 |
| 2 |
| 3 |
| 2 |
| 1000 |
| x1 |
| 1000 |
| x1 |
| 1000 |
| x1 |
| g(x)+g(x2) |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com