
题目列表(包括答案和解析)
| 分数(分数段) | 频数(人数) | 频率 |
| [60,70) | 9 | x |
| [70,80) | y | 0.38 |
| [80,90) | 16 | 0.32 |
| [90,100) | z | s |
| 合 计 | p | 1 |
| 分数(分数段) | 频数(人数) | 频率 |
| [60,70) | 9 | x |
| [70,80) | y | 0.38 |
| [80,90) | 16 | 0.32 |
| [90,100) | z | s |
| 合 计 | p | 1 |
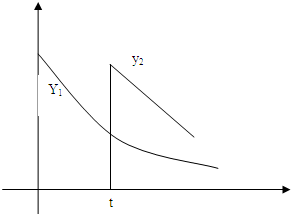 心理学家研究某位学生的学习情况发现:若这位学生刚学完的知识存留量为1,则x天后的存留量y1=
心理学家研究某位学生的学习情况发现:若这位学生刚学完的知识存留量为1,则x天后的存留量y1=| 4 |
| x+4 |
| a |
| (t+4)2 |
 已知函数f(x)=x2-2|x|-1的图象,并写出该函数的单调区间与值域.
已知函数f(x)=x2-2|x|-1的图象,并写出该函数的单调区间与值域.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com