
题目列表(包括答案和解析)
(本小题满分12分)在我校值周活动中,甲、乙等五名值周生被随机地分到A,B,C,D四个不同的岗位服务,每个岗位至少有一名值周生.
(1)求甲、乙两人同时参加A岗位服务的概率;
(2)求甲、乙两人不在同一个岗位服务的概率;
(3)设随机变量X为这五名值周生中参加A岗位服务的人数,求X的分布列及期望.
(本小题满分12分)
为了加快经济的发展,某市选择A、B两区作为龙头带动周边地区的发展,决定在A、B两区的周边修建城际快速通道,假设A、B两区相距 个单位距离,城际快速通道所在的曲线为E,使快速通道E上的点到两区的距离之和为4个单位距离.
个单位距离,城际快速通道所在的曲线为E,使快速通道E上的点到两区的距离之和为4个单位距离.

(Ⅰ)以线段AB的中点O为原点建立如图所示的直角坐标系,求城际快速通道所在曲线E的方程;
(Ⅱ)若有一条斜率为 的笔直公路l与曲线E交于P,Q两点,同时在曲线E上建一个加油站M(横坐标为负值)满足
的笔直公路l与曲线E交于P,Q两点,同时在曲线E上建一个加油站M(横坐标为负值)满足 ,求
,求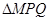 面积的最大值.
面积的最大值.
(本小题满分12分)
某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:在C处进行该仪器的垂直弹射,观测点A、B两地相距100米,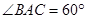 ,在A地听到弹射声音的时间比B地晚
,在A地听到弹射声音的时间比B地晚 秒,A地测得该仪器在A、B、C三地位于同一水平面上,至最高点H时的仰角为30°,求该仪器的垂直弹射高度CH(声音的传播速度为340米/秒)
秒,A地测得该仪器在A、B、C三地位于同一水平面上,至最高点H时的仰角为30°,求该仪器的垂直弹射高度CH(声音的传播速度为340米/秒)
(本小题满分12分)
在一次体操选拔赛中,教练组设置了难度不同的甲、乙两个系列,每个系列都有A和B两个动作.比赛时每位运动员自选一个系列完成,两个动作得分之和为该运动员的成绩.
假设每个运动员完成每个系列中的两个动作的得分是相互独立的.根据赛前训练统计数据,某运动员完成甲系列和乙系列的情况如下表:
表1:甲系列 表2:乙系列
|
|
现该运动员最后一个出场,之前其他运动员的最高得分为115分.
(Ⅰ)若该运动员希望获得该项目的第一名,应选择哪个系列?说明理由,并求其获得第一名的概率;
(Ⅱ)若该运动员选择乙系列,求其成绩 的分布列及其数学期望
的分布列及其数学期望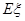 .
.
(本小题满分12分)
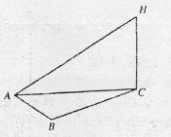
如图: 正在海上A处执行任务的渔政船甲和在B处执行任务的渔政船乙,同时收到同一片海域上一艘渔船丙的求救信号,此时渔船丙在渔政船甲的南偏东40°方向距渔政船甲70km的C处,渔政船乙在渔政船甲的南偏西20°方向的B处,两艘渔政船协调后立即让
正在海上A处执行任务的渔政船甲和在B处执行任务的渔政船乙,同时收到同一片海域上一艘渔船丙的求救信号,此时渔船丙在渔政船甲的南偏东40°方向距渔政船甲70km的C处,渔政船乙在渔政船甲的南偏西20°方向的B处,两艘渔政船协调后立即让 渔政船甲向渔船丙所在的位置C处沿直线AC航行前去救援,渔政船乙仍留在B处执行任务,渔政船甲航行30km到达D处时,收到新的指令另有重要任务必须执行,于是立即通知在B处执行任务的渔政船乙前去救援渔船丙(渔政船乙沿直线BC航行前去救援渔船丙),此时B、D两处相距42km,问渔政船乙要航行多少距离才能到达渔船丙所在的位置C处实施营救.
渔政船甲向渔船丙所在的位置C处沿直线AC航行前去救援,渔政船乙仍留在B处执行任务,渔政船甲航行30km到达D处时,收到新的指令另有重要任务必须执行,于是立即通知在B处执行任务的渔政船乙前去救援渔船丙(渔政船乙沿直线BC航行前去救援渔船丙),此时B、D两处相距42km,问渔政船乙要航行多少距离才能到达渔船丙所在的位置C处实施营救.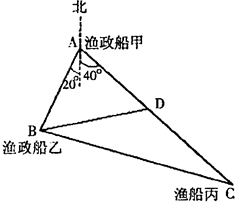
一、选择题
1.D 2.A 3.A 4.B 5.B 6.C 7.C 8.C 9.C 10.B 11.D 12.A
二、填空题
13. 14. 15. 16.③④
三、解答题
17.解:(1)将得
(2)不等式即为
即
①当
②当
③.
18.解:
19.解:(1)设正面出现的次数为m,反面出现的次数为n,则,可得:
(2)
20.解法(一)
(1)证明:∵AE⊥平面AA1DD1,A1D⊥AD1,∴A1D⊥D1E
(2)设点E到面ACD1的距离为h,在△ACD1中,AC=CD1=,AD1=,
故
(3)过D作DH⊥CE于H,连D1H、DE,则D1H⊥CE,
∴∠DHD1为二面角D1―EC―D的平面角.
设AE=x,则BE=2-x
解法(二):以D为坐标原点,直线DA,DC,DD1分别为x,y,z轴,建立空间直角坐标系,设AE=x,则A1(1,0,1),D1(0,0,1),E(1,x,0),A(1,0,0)C(0,2,0)
(1)
(2)因为E为AB的中点,则E(1,1,0),从而,
,设平面ACD1的法向量为,则
也即,得,从而,所以点E到平面AD1C的距离为
(3)设平面D1EC的法向量,∴
由 令b=1, ∴c=2,a=2-x,
∴
依题意
∴(不合,舍去), .
∴AE=时,二面角D1―EC―D的大小为.
21.解:(1)方法一 用数学归纳法证明:
1°当n=1时,
∴,命题正确.
2°假设n=k时有
则
而
又
∴时命题正确.
由1°、2°知,对一切n∈N时有
方法二:用数学归纳法证明:
1°当n=1时,∴;
2°假设n=k时有成立,
令,在[0,2]上单调递增,所以由假设
有:即
也即当n=k+1时 成立,所以对一切
(2)下面来求数列的通项:所以
,
又bn=-1,所以
22.解:(1)设切点A、B坐标分别为,
∴切线AP的方程为:
切线BP的方程为:
解得P点的坐标为:
所以△APB的重心G的坐标为 ,
所以,由点P在直线l上运动,从而得到重心G的轨迹方程为:
(2)方法1:因为
由于P点在抛物线外,则
∴
同理有
∴∠AFP=∠PFB.
方法2:①当所以P点坐标为,则P点到直线AF的距离为:
即
所以P点到直线BF的距离为:
所以d1=d2,即得∠AFP=∠PFB.
②当时,直线AF的方程:
直线BF的方程:
所以P点到直线AF的距离为:
,同理可得到P点到直线BF的距离,因此由d1=d2,可得到∠AFP=∠PFB.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com