
题目列表(包括答案和解析)
(本小题满分12分)已知锐角 中内角
中内角 、
、 、
、 的对边分别为
的对边分别为 、
、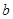 、
、 ,且
,且 .
.
(1)求角 的值;
的值;
(2)设函数 ,
, 图象上相邻两最高点间的距离为
图象上相邻两最高点间的距离为 ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)
已知向量 ,向量
,向量 ,函数
,函数 .
.
(Ⅰ)求 的最小正周期
的最小正周期 ;
;
(Ⅱ)已知 ,
, ,
, 分别为
分别为 内角
内角 ,
, ,
, 的对边,
的对边, 为锐角,
为锐角, ,且
,且
恰是 在
在 ,
, 
 上的最大值,求
上的最大值,求 ,
, 和
和 的面积.
的面积.
(本小题满分12分)
已知向量 ,
, ,向量
,向量 ,
, ,函数
,函数 .
.
(Ⅰ)求 的最小正周期
的最小正周期 ;
;
(Ⅱ)已知 ,
, ,
, 分别为
分别为 内角
内角 ,
, ,
, 的对边,
的对边, 为锐角,
为锐角, ,
, ,且
,且 恰是
恰是 在
在 ,
, 上的最大值,求
上的最大值,求 ,
, 和
和 的面积
的面积 .
.
(本小题满分14分)
如图,直线 和
和 相交于点
相交于点 且
且 ,点
,点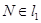 .以
.以 为端点的曲线段C上的任一点到
为端点的曲线段C上的任一点到 的距离与到点
的距离与到点 的距离相等.若
的距离相等.若 为锐角三角形,
为锐角三角形, ,
, ,且
,且 .
.
(1)曲线段C是哪类圆锥曲线的一部分?并建立适当的坐标系,求曲线段C所在的圆锥曲线的标准方程;
(2)在(1)所建的坐标系下,已知点 在曲线段C上,直线
在曲线段C上,直线 ,求直线
,求直线 被圆
被圆 截得的弦长的取值范围.
截得的弦长的取值范围.

(本小题满分12分)已知锐角 中内角
中内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且
,且 .
.
(1)求角 的值;
的值;
(2)设函数 ,
, 图象上相邻两最高点间的距离为
图象上相邻两最高点间的距离为 ,求
,求 的取值范围.
的取值范围.
一 选择题
(1)B (2)C (3)B (4)B (5)D (6)A
(7)A (8)C (9)D (10)C (11)B (12)C
二 填空题
(13)(老课程).files\image153.png) (14)
(14)(老课程).files\image155.png) (15)
(15)(老课程).files\image157.png) (16)1
(16)1
三、解答题
(17)本小题主要考查指数和对数的性质以及解方程的有关知识. 满分12分.
解:(老课程).files\image159.png)
(老课程).files\image161.png)
(老课程).files\image163.png) (无解). 所以
(无解). 所以(老课程).files\image165.png)
(18)本小题主要考查同角三角函数的基本关系式、二倍角公式等基础知识以及三角恒等变形的能力. 满分12分.
解:原式(老课程).files\image167.png)
因为 (老课程).files\image169.png)
所以 原式(老课程).files\image171.png) .
.
因为(老课程).files\image173.png) 为锐角,由
为锐角,由(老课程).files\image175.png) .
.
所以 原式(老课程).files\image177.png)
因为(老课程).files\image173.png) 为锐角,由
为锐角,由(老课程).files\image179.png)
所以 原式(老课程).files\image177.png)
(19)本小题主要考查等差数列的通项公式,前n项和公式等基础知识,根据已知条件列方程以及运算能力.满分12分.
解:设等差数列(老课程).files\image136.png) 的公差为d,由
的公差为d,由(老课程).files\image181.png) 及已知条件得
及已知条件得
(老课程).files\image183.png) , ①
, ①
(老课程).files\image185.png) ②
②
由②得(老课程).files\image187.png) ,代入①有
,代入①有(老课程).files\image189.png)
解得 (老课程).files\image191.png) 当
当(老课程).files\image193.png) 舍去.
舍去.
因此 (老课程).files\image195.png)
故数列(老课程).files\image136.png) 的通项公式
的通项公式(老课程).files\image198.png)
(老课程).files\image200.png)
(20)本小题主要考查把实际问题抽象为数学问题,应用不等式等基础知识和方法解决问题的能力. 满分12分.
解:设矩形温室的左侧边长为a m,后侧边长为b m,则(老课程).files\image202.png)
蔬菜的种植面积
(老课程).files\image204.png)
(老课程).files\image206.png)
所以(老课程).files\image208.png)
当(老课程).files\image210.png)
答:当矩形温室的左侧边长为40m,后侧边长为20m时,蔬菜的种植面积最大,最大种植面积为648m2.
(老课程).files\image211.png) (21)本小题主要考查两个平面垂直的性质、二面角等有关知识,以有逻辑思维能力和空间想象能力. 满分12分.
(21)本小题主要考查两个平面垂直的性质、二面角等有关知识,以有逻辑思维能力和空间想象能力. 满分12分.
|