
题目列表(包括答案和解析)
(本题满分12分)在四棱锥P—ABCD中,底面ABCD是a的正方形,PA⊥平面ABCD,且PA=2AB
(Ⅰ)求证:平面PAC⊥平面PBD;
(Ⅱ)求二面角B—PC—D的余弦值.

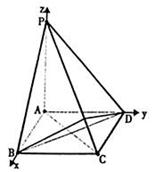
(本题满分12分)在四棱锥P—ABCD中,底面ABCD是a的正方形,PA⊥平面ABCD,且PA=2AB
(Ⅰ)求证:平面PAC⊥平面PBD;
(Ⅱ)求二面角B—PC—D的余弦值.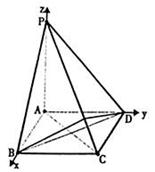
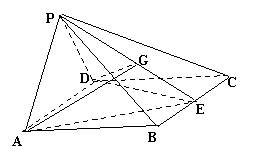 (本小题满分12分)、四棱锥P—ABCD中,侧面PAD
(本小题满分12分)、四棱锥P—ABCD中,侧面PAD![]() 底面ABCD,底面ABCD是边长为2的正方形,又PA=PD,
底面ABCD,底面ABCD是边长为2的正方形,又PA=PD,![]() ,E、G分别是BC、PE的中点。
,E、G分别是BC、PE的中点。
(1)求证:AD![]() PE;
PE;
(2)求二面角E—AD—G的正切值。
(本题满分12分)
如图,四棱锥P-ABCD的侧面PAD垂直于底面ABCD,∠ADC=∠BCD= ,PA=PD=AD=2BC=2,CD
,PA=PD=AD=2BC=2,CD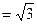 ,M在棱PC上,N是AD的中点,二面角M-BN-C为
,M在棱PC上,N是AD的中点,二面角M-BN-C为 .
.
(1)求 的值;
的值;
(2)求直线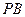 与平面BMN所成角的大小.[来源:学科网
与平面BMN所成角的大小.[来源:学科网 ZXXK]
ZXXK]
一、选择题:(本大题共12小题每小题5分,共60分)
AADCB DDBCC DC
二、填空题:(共4小题,每小题4分,共16分)
13. 14.20 15.32 16.
14.20 15.32 16.
三、解答题:(共6小题,共74分)
17.解:(1) ………………2分
………………2分
 .………………………………4分
.………………………………4分
在[0,π]上单调递增区间为 .…………………6分
.…………………6分
(2) ,
,
当x=0时, ,………………………………………8分
,………………………………………8分
由题设知 …………………………………………10分
…………………………………………10分
解之,得 …………………………………………12分
…………………………………………12分
|