练习册

  • 练习册
  • 试题
    (A) (B)- (C)4 (D)-4 【查看更多】

     

    题目列表(包括答案和解析)

    （06年湖北卷文）已知非零向量a、b，若a＋2b与a－2b互相垂直，则（ ）

    A.                B.  4              C.               D. 2

    查看答案和解析>>

    （3）某人5次上班途中所花的时间（单位：分钟）分别为x，y，10，11，9.已知这组数据的平均数为10，方差为2，则|x－y|的值为

    （A）1　　　　（B）2　　　　　（C）3　　　　　（D）4

    查看答案和解析>>

    （4）对于向量，a 、b、c和实数，下列命题中真命题是

    A 若ab=0，则a＝0或b＝0         B 若，则λ＝0或a＝0

    C 若＝，则a＝b或a＝－b     D 若，则b＝c

    查看答案和解析>>

    （辽宁理，4）已知圆C与直线x－y=0 及x－y－4=0都相切，圆心在直线x+y=0上，则圆C的方程为

    A.          B.

    C.          D.

    查看答案和解析>>

    （本小题满分10分）选修4－1《几何证明选讲》．
    已知A、B、C、D为圆O上的四点，直线DE为圆O的切线，AC∥DE，AC与BD相交于H点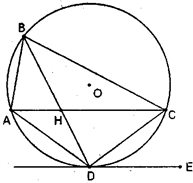

    （Ⅰ）求证：BD平分∠ABC
    （Ⅱ）若AB＝4，AD＝6，BD＝8，求AH的长．

    查看答案和解析>>

     

    一．选择题

    （1）D      （2）A     （3）B       （4）C       （5）B     （6）C

    （7）B      （8）C     （9）A       （10）C      （11）B    （12）D

    二．填空题

    （13）4   （14）0.75   （15）9    （16）

    三．解答题

    （17）解：由

                                 

    得    又

    于是 

          

    （18）解：（Ⅰ）设A、B、C分别为甲、乙、丙三台机床各自加工的零件是一等品的事件.

    ①

    ②

    ③

      由①、③得  代入②得  27[P(C)]2－51P(C)+22=0.

    解得  （舍去）.

    将     分别代入 ③、②  可得 

    即甲、乙、丙三台机床各加工的零件是一等品的概率分别是

    （Ⅱ）记D为从甲、乙、丙加工的零件中各取一个检验，至少有一个一等品的事件，

    则 

    故从甲、乙、丙加工的零件中各取一个检验，至少有一个一等品的概率为

     

    （19）（Ⅰ）证明  因为底面ABCD是菱形，∠ABC=60°，

    由PA2+AB2=2a2=PB2   知PA⊥AB.

    同理，PA⊥AD，所以PA⊥平面ABCD.

    （Ⅱ）解  作EG//PA交AD于G，

    由PA⊥平面ABCD.

    知EG⊥平面ABCD.作GH⊥AC于H，连结EH，

    则EH⊥AC，∠EHG即为二面角的平面角.

    又PE : ED=2 : 1，所以

    从而    

    （Ⅲ）解法一  以A为坐标原点，直线AD、AP分别为y轴、z轴，过A点垂直平面PAD的直线为x轴，建立空间直角坐标系如图.由题设条件，相关各点的坐标分别为

    所以

    设点F是棱PC上的点，则

           令   得

    解得      即 时，

    亦即，F是PC的中点时，、、共面.

    又  BF平面AEC，所以当F是棱PC的中点时，BF//平面AEC.

    解法二  当F是棱PC的中点时，BF//平面AEC，证明如下，

    由   知E是MD的中点.

    连结BM、BD，设BDAC=O，则O为BD的中点.

    所以  BM//OE.  ②

    由①、②知，平面BFM//平面AEC.

    又  BF平面BFM，所以BF//平面AEC.

    证法二

    因为 

             

    所以  、、共面.

    又 BF平面ABC，从而BF//平面AEC.

    （20）解：（Ⅰ）

    （i）当a=0时，令

    若上单调递增；

    若上单调递减.

    （ii）当a<0时，令

    若上单调递减；

    若上单调递增；

    若上单调递减.

    （Ⅱ）（i）当a=0时，在区间[0，1]上的最大值是

    （ii）当时，在区间[0，1]上的最大值是.

    （iii）当时，在区间[0，1]上的最大值是

    （21）解：（Ⅰ）依题意，可设直线AB的方程为 代入抛物线方程得   

         ①

    设A、B两点的坐标分别是 、、x2是方程①的两根.

    所以     

    由点P（0，m）分有向线段所成的比为，

    得

    又点Q是点P关于原点的对称点，

    故点Q的坐标是（0，－m），从而.

                   

                   

    所以 

    （Ⅱ）由 得点A、B的坐标分别是（6，9）、（－4，4）.

    由   得

    所以抛物线 在点A处切线的斜率为

    设圆C的方程是

    则

    解之得

    所以圆C的方程是 

    即 

    （22）（Ⅰ）证明：设点Pn的坐标是，由已知条件得

    点Qn、Pn+1的坐标分别是：

    由Pn+1在直线l1上，得 

    所以    即 

    （Ⅱ）解：由题设知 又由（Ⅰ）知 ，

    所以数列  是首项为公比为的等比数列.

    从而 

    （Ⅲ）解：由得点P的坐标为（1，1）.

    所以 

       

    （i）当时，>1+9=10.

    而此时 

    （ii）当时，<1+9=10.

    而此时 

     


    同步练习册答案